k=1 L = lim k=1 ˆ j dx sgn GL = i
|
|
|
- Sander Borgen
- 5 år siden
- Visninger:
Transkript
1 Ë Ò Ô ÐÐÓÚ Ö Ø Ù Ð Ò ÓÒ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Å Ö ÙÒ Ý ÂÓ Ò À ÖÚ Ý È ÖÖ Ë ÐÓ + ÎÐ Ñ Ö ÎÓÐ ÓÚ Ì Ñ Ò Ò Ë ÓÓÐ Ó Ù Ò Ò ÓÒÓÑ ÍÒ Ú Ö ØÝ Ó Ì Ñ Ò +Ï Ð Ö Ä ÙÖ Ö ÍÒ Ú Ö ØÝ ÂÙÐÝ ¾¼½ ØÖ Ø Ì Ô ÐÐÓÚ Ö Ø Ó ÒØ ÖÓÒÒ Ø Ò ØÛ Ò Ò Ò Ð Ø ÓÑÔÓ ÒØÓ ÓØ ÓÙÖ Ó Ó Ò Û Ø Ö Ø Ý ÑÔÐ Ý ÓÖ ÑÔ Ò ÚÓÐ Ø Ð ØÝ ÓÒ Ø ÓÒ Ò Ø Ø Ö Ø Ñ Ö Øº Ï Ù ØÓÖ Ð ÓÑÔÓ Ø ÓÒ ØÓ Ö ÖÖ Ò Ò ÓÖÑ Ø ÓÒ ÖÓÑ Î Ê Û ÒÐÙ ÓÙÖ Ö Ø ÓÒ Ò Ò Ó Ø Ù Ð Ò ÓÒ Ø ÙÒ Ò ÓÖ Ø ÖÖÓÖ Ú Ö Ò ÓÑÔÓ Ø ÓÒ ÔÔÖÓ Ó ÓÐ Ò ÐÑ Þ ¾¼¼ µº Ô ÐÐÓÚ Ö Ò Ü ÓÒ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ ÑÔÐ ÝÑÔØÓØ ÔÖÓÔ ÖØ Ô ÖÑ ØØ Ò Ø Ö Ú Ø ÓÒ Ó Ò ÐÝØ Ð Ø Ò Ö ÖÖÓÖ Ó Ø Ò Ü Ò Ø ÓÑÔÓÒ ÒØ º Ï ÔÔÐÝ Ø Ñ Ø Ó ÓÐÓ Ý ØÓ Ô Ò Ð Ó Ë ÔÖ Ó ÓÚ Ö Ò Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ ÓÖ Ø Ô Ö Ó ¾¼¼ ¹¾¼½ Ò ÒØ Ý ÓÛ Ø ÒØ Ø ÓÒØÖ ÙØ ØÓ ÐÓ Ð Ý Ø Ñ Ö º à ÝÛÓÖ À ØÓÖ Ð ÓÑÔÓ Ø ÓÒ ËÔ ÐÐÓÚ Ö Ö Ò Ö Ù Ð ØÝ Æ ØÛÓÖ Â Ä Ð Ø ÓÒ ÆÙÑ Ö ¾ ½ ¾ ½¼ ÒÓÛÐ Ñ ÒØ ÙÒ Ý Ò ÎÓÐ ÓÚ ÒÓÛÐ ÙÒ Ò ÖÓÑ Ê È½ ¼½¼½ ½ º Ï Ö Ö Ø ÙÐ ÓÖ ÓÑÑ ÒØ ÖÓÑ Ô ÖØ Ô ÒØ Ø Ø ¾¼½ ËÓ ÓÒ Ö Ò Ò Æ Û ÓÖ º ÓÖÖ ÔÓÒ Ò ÙØ ÓÖ Å Ö ÙÒ Ý Ì Ñ Ò Ò Ë ÓÓÐ Ó Ù Ò Ò ÓÒÓÑ ÍÒ Ú Ö ØÝ Ó Ì Ñ Ò ÈÖ Ú Ø ÀÓ ÖØ Ì Ñ Ò ¼¼½ Ù ØÖ Ð º Ñ Ð Ñ Ö º ÙÒ ÝÙØ º Ùº Ù ½
2 ½ ÁÒØÖÓ ÙØ ÓÒ Ø ÖÑ Ò Ò Ø ÙÐØ Ñ Ø ÓÙÖ Ó Ó Ò ÓÑÔÐ Ü Ý Ø Ñ Ó ÒØ Ö Ø Ò ÒØ Ø ÔÓРݹ Ñ Ò Ò ÖÚ Ò º Á Ø ÓÙÖ µ Ò ÕÙ ÐÝ ÒØ Û Ø ÖØ ÒØÝ Ø Ò ÔÓÐ Ý Ò Ø Ú ÐÝ Ñ Ø ÒÙ Ò ÓÖ ÐÐ Ú Ø Ò Ö ÓÖ ÒÓÒ¹ Ö ÓÙØÓÑ º Ì Ò Ó ÙÒ Ö Ø Ò Ò Ø ÓÑÔÐ Ü ÒØ Ö Ø ÓÒ Ò Ø ÓÒÓÑÝ Ô ÖØ Ó Ø ÜÔ Ò Ò Ð Ø Ö ØÙÖ ÓÒ ÓØ ÓÒÓÑ Ò Ò Ò Ð Ò ØÛÓÖ ÓÖ Ü ÑÔÐ ÑÓ ÐÙ Ø Ðº ¾¼½¾µ ÑÓ ÐÙ Ø Ðº ¾¼½ µ È Ö Ò Ò Ò ¾¼½ µ Ò ÓÐ Ò ÐÑ Þ ¾¼½ µº ÓÒ ÔØ Ó ÒØ ÖÓÒÒ Ø Ò ÔÐ Ý Ò Ý ÖÓÐ Ò ÙÒ Ö Ø Ò Ò Ò Ò Ð Ò ØÛÓÖ ÐÙ Ú Ò Ö ÕÙ Ö ÑÓÖ ØØ ÒØ ÓÒº ÌÓ Ø Ñ Ø Ò ØÛÓÖ Ô ÐÐÓÚ Ö ÑÔ Ö ÐÐÝ Ø Ñ Ø Ó Ó ÓÐ Ò ÐÑ Þ ¾¼¼ µ Ò ÓÖØ ÓÖ Ñ ÙÖ Ò Ø Ö Ð Ø Ú ÓÒØÖ ÙØ ÓÒ Ó Ó ÖÓÑ ÐØ ÖÒ Ø Ú ÓÙÖ Ô ÐÐ Ò ÓÚ Ö ØÓ Ø ÓØ Ö ÓÑÑÓÒ Ò Ø Ð Ø Ö ØÙÖ º ÁÒ Ø Ñ Ø Ó ÒØ ÖÓÒÒ Ø Ò Ó Ø Ò ØÛÓÖ Ò ÖÓÑ ÓÖ Ø ÖÖÓÖ Ú Ö Ò ÓÑÔÓ Ø ÓÒ ÓÒ Ø Ò Ö Ú ØÓÖ ÙØÓ¹Ö Ö ÓÒ Ö Ñ ÛÓÖ ØÛ Ò Ò Ó ÒÓÙ Ú Ö Ð ÓÐ Ò ÐÑ Þ ¾¼½ µµº Ì ÔÔÖÓ Ò ÔÓÔÙÐ Ö ØÝ Û Ø Ø Ú ÒØ Ó Ò Ý ØÓ ÑÔÐ Ñ ÒØ Ò ÒØ ÖÔÖ Ø Ñ Ò ÐÝ Ò ÓÖ Ø Ò ÔÖÓÔ ÖØ ÑÔÐ ÜØ Ò ÓÒ ØÓ Ú ÖÝ Ò Ø Ñ ÓÖ ÞÓÒ Ò ÔÔÐ Ð ÖÓ Ñ ÒÝ Ö ÒØ ØÝÔ Ó ÔÔÐ Ø ÓÒ ÓÖ Ü ÑÔÐ ÐÑ Þ ¾¼½¼µ ÐØ Ö Ò Ý Ö ¾¼½ µ Ò Ø Ö Ò Ó ÔÔÐ Ø ÓÒ ÔÖ ÒØ Ò ÓÐ Ò ÐÑ Þ ¾¼½ µ Ò Ñ Ö Ö Ø Ðº ¾¼½ µº Ì Ô Ô Ö ÔÖÓÔÓ ÙÖØ Ö Ú ÐÓÔÑ ÒØ Û Ø Ø ÓÒ Ð Ú ÒØ Ó Ò Ò Ø ÓÒ¹ ØÖ ÙØ ÓÒ Ó Ø ÓÙÖ Ó ÚÓÐ Ø Ð ØÝ ÒØÓ Ø Ó Û Ù Ñ ÒØ Ó ÖÚ ÚÓÐ Ø Ð ØÝ Ò Ø Ó Û ÑÔ Ò Øº Ï Ó Ø Ý Ö ÖÖ Ò Ò Ø Ò ÓÖÑ Ø ÓÒ Ò Ø Ø Ò Ö Ú ØÓÖ ÙØÓ¹Ö Ö ÓÒ ØÓ Ø Ú ÒØ Ó Ø Ó¹ ÐÐ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ø Ø Ø º Ì ÓÑÔÓ Ø ÓÒ Óй ÐÓÛ ÖÓÑ Ø Î ÊÅ ÓÖÑ Ó Ø Ö Ù Ð Ò Ø Î Ê ØÓ ØØÖ ÙØ Ø Ø Ñ Ø Ú ÐÙ Ó Ò Ó ÖÚ Ø ÓÒ ØÓ Ø ÓÑÔÓÒ ÒØ Ó º À ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ú Ò Ù ÔÖ Ú ÓÙ ÐÝ Ò Ø Ñ ÖÓ ÓÒÓÑ Î Ê Ð Ø Ö ØÙÖ Ù ÙÒ Ý Ò È Ò ¾¼¼¼µ Ë Ñ ½ ¾µ ÙØ ØÓ ÓÙÖ ÒÓÛÐ Ú ÒÓØ Ò ÔÔÐ Ò Ø Û Ý ÔÖÓÔÓ Ò Ø Ô Ô Öº Ì ØÓÖ Ð ÓÑÔÓ¹ Ø ÓÒ ÔÔÖÓ ØÓ ÓÑÔÓ Ò Ø ÓÙÖ Ó Ó Ò Ñ ÙÖ Ò ÒØ ÖÓÒÒ Ø Ò Ó ÒÓØ Ö ÕÙ Ö ÒÓÖÑ Ð Þ Ø ÓÒ ÙÑÔØ ÓÒ ÒÓÖ Ò Ö Ðݵ Ó Ó Û Ò ÓÛ Ð Ò Ø ØÓ Ó Ø Ò Ø Ñ ¹Ú ÖÝ Ò Ô ÐÐÓÚ Ö Ò Ü Ò Ñ Ø Ó ¹ ÐØ ÓÙ Ø Ò ÓÑÑÓ Ø Ö º ÙÑ Ò ÝÑÔØÓØ ÒÓÖÑ Ð ØÝ Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ð Ñ ÒØ Ú Ø Ú ÔÖÓÔ ÖØ Ó Ø Ø Û Ò Ó Ø Ò ÒÓØ ÓÒÐÝ Ø ØÓØ Ð ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ô ÐÐÓÚ Ö Ò Ü ÖÓÑ Ô ÖØ ¹ ÙÐ Ö ÓÙÖ ØÓ Ú Ò ÒØ ØÝ ÙØ Ð Ó ÓÒØÖ ÙØ ÓÒ Ó Ù Ø Ó ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ò ÓÒ Ò Ò ÓÖ ÓØ º Ï ÔÖÓÚ ÙÖØ Ö Ò Ø ÒØÓ Ø ÖÓÐ Ó Ó Ø Ø ÒÓØ Ú ÒØ ÖÓÑ ÙÒ Ò Óѹ ÔÓ Ø ÓÒ º Ì ÔÔÐ Ø ÓÒ Ò Ø Ô Ô Ö ØÓ Ø Ó ½¼ Ö Ø ÙÐØ Û Ô Ëµ ÔÖ ÓÖ Ð Ø ÓÒ Ó Ò Ò Ð Ò Ø ØÙØ ÓÒ Ò ÓÚ Ö Ò Ù Ò Ý Ö Ø ÒÓÑ Ò Ø Ò ÍË ÓÐÐ Ö ÓÚ Ö Ø Ô Ö Ó ¾¼¼ ¹¾¼½ º Ì Ö ÙÐØ ØÖ Ø Ø Ñ ¹Ú ÖÝ Ò ÓÒØÖ ÙØ ÓÒ Ó Ù ØÓÖ Ó Ø Ø ØÓ ÓÚ Ö ÐÐ ÔÖ º ÓÖ Ü ÑÔÐ Û ÓÛ Ø Ø Ø Ò Ò ØÓÖ Ò Ö ÐÐÝ Ø ØÓ Ü Ö Ø ÔÖ ÙÖ Ò Ø Ô Ö Ó Ó Ø ÐÓ Ð Ò Ò Ð Ö º Ò Ò Ð Ò Ø ØÙØ ÓÒ Ö Ø Ñ ÓÖ Ö Ô ÒØ Ó Ó ÙÖ Ò Ø Ò Ø ÙÖÓÔ Ò Ø Ö º Ñ Ö Ò ¾
3 Ò ÖÓÒØ Ö Ñ Ö Ø Ö ØÖÓÒ ÐÝ ÒØ ÖÓÒÒ Ø Û Ð Ø ØÖ Ò Ñ ÓÒ ÖÓÑ Ø Ñ Ö Ø ØÓ Ú ÐÓÔ Ñ Ö Ø Ö Ö Ð Ø Ú ÐÝ Ñ Ðк ÐÓ Ð Ý Ø Ñ ÐÐÝ ÑÔÓÖØ ÒØ Ò Ö Ø ÑÓ Ø Ò Ù ÒØ Ð ÒØ Ø Ù Ò ÓØ Ö Ò Ö Ø Ð Ð Ò Ò Ø ÓÑ Ò Ò ØÛÓÖ º Ï Ð Ó ÓÛ Ø Ø Ö ÓÖ Ö ÑÓÑ ÒØ Ó Ø Ô ÐÐÓÚ Ö ÓÒØ Ò Ö Ò Ò ÓÖÑ Ø ÓÒ ÓÙØ Ø ÚÓÐÙØ ÓÒ Ó Ø Ô ÐÐÓÚ Ö Ò Ü ÓÚ Ö Ø Ñ º Ì Ö Ñ Ò Ö Ó Ø ÖØ Ð ÓÖ Ò Þ ÓÐÐÓÛ º Ë Ø ÓÒ ¾ ÒØÖÓ Ù ÒÓÚ Ð ÒØ ÖÓÒÒ Ø ¹ Ò Ñ ÙÖ Û Ø ÒØÓ ÓÙÒØ Ø Ó Ò Û Ø Ö Ø Ó ÑÔÐ Ý ÓÖ ÑÔ Ò ÚÓÐ Ø Ð ØÝ Ò Ø Ø Ö Ø Ñ Ö Ø Ò ÔÖÓÚ ÝÑÔØÓØ ÔÖÓÔ ÖØ Ó Ø Ñ ÙÖ º Ë Ø ÓÒ ÓÙع Ð Ò Ø Ø Ø ÓÒ Ø Ò Ó ÐÝ Ë ÔÖ ÓÖ ÓÚ Ö Ò Ò Ø ÓÒ Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ º Ë Ø ÓÒ Ù Ø ÑÔ Ö Ð Ö ÙÐØ º Ë Ø ÓÒ ÓÒÐÙ º ¾ Å ÙÖ Ò ÒØ ÖÓÒÒ Ø Ò ÖÓÑ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ì Ñ Ø Ó ÓÐÓ Ý ÔÖÓÔÓ Ö ÔÖÓÚ Ò Û Ñ ÙÖ Ó ÒØ ÖÓÒÒ Ø Ò Ý ÑÓ Ý Ò Ø ÓÐ Ò ÐÑ Þ ¾¼¼ µ ÔÔÖÓ º Ý ÓÙ Ò ÓÒ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ö Ø Ö Ø Ò ÓÖ Ø ÖÖÓÖ Ú Ö Ò ÓÑÔÓ Ø ÓÒ Û ÔÖÓÚ Ø Ò Ó ÓÒØÖ ÙØÓÖÝ Ó Ò Ò¹ ÓÖÑ Ø ÓÒ ÓÒ Û Ø Ö ØÖ Ò Ñ ÓÒ Ù Ñ ÒØ ÓÖ ÑÔ Ò Ø ÓÙØÓÑ Ò Ø Ø Ö Ø Ñ Ö Øº ¾º½ Æ ØÛÓÖ Ó ÓÚ Ö Ò Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ ÓÒ Ö N ÒØ Ø Ò Ü Ý i N 1 Ó Ø ÒØ Ø Ö Ò Ò Ð Ò Ø ØÙØ ÓÒ Û Ð Ò ÓÖ ÔÖÓ Ø Û Ø ÙÒ ÖØ Ò Ö ØÙÖÒ Ò ÑÓÒ ½ ¾µ Ò N 2 Ö ÓÚ Ö Ò ÓÖÖÓÛ Ö Û Ö N N 1 +N 2 º Ì Ò Ò Ð Ò Ø ØÙØ ÓÒ ÒÒÓØ ÙÒ Ø Ö Ð Ò Ò Ø Ú Ø ÖÓÑ Ø Ö ÓÛÒ Ð Ò Ø Ò Ø Ð ÒØ Ö¹ Ò Ø ØÙØ ÓÒ Ð ÓÛ Û Ø ÓØ Öº ÓÐÐÓÛ Ò ÑÓ ÐÙ Ø Ðº ¾¼½ µ Ò Ò Ð Ò Ø ØÙØ ÓÒ Ø ÓÔÔÓÖØÙÒ ØÝ ØÓ ÒÚ Ø Ò Ø Ö Ð ÓÒÓÑÝ Û Ø Ò ÙÒ ÖØ Ò Ö ØÙÖÒ r 1,it Ò Ô Ö Ó t Ò»ÓÖ ÒÚ Ø Ò ÓÚ Ö Ò ÓÒ Û Ø r 2,it º ÁÒÓÖÔÓÖ Ø Ò Ø ÜØ Ò ÓÒ ÔÖÓÔÓ Ý ÙÒ Ý Ø Ðº ¾¼½ µ ÓÚ Ö Ò ÓÒ Ö ØÙÖÒ r 2,it Ð Ó Ö Ý Ò Ø Ú ÐÙ Ó Ö ØÙÖÒ r 1,it Ò r 2,it Ö Ò Ù Ò Ý Ò ÜØ ÖÒ Ð Ó u it Û Ö Ò ÓÑ Ú Ö Ð Ö ÛÒ ÖÓÑ Ú Ò ØÖ ÙØ ÓÒ Û Ø Ñ Ò Þ ÖÓ Ò Ú Ö Ò ÓÒ º ½ Ì Ó ÒØ ÔÖÓ Ð ØÝ ØÖ ÙØ ÓÒ p(u 1t,...,u Nt ) ÓÖ N ÒØ Ø ÙÑ ØÓ ÒÓÛÒº Ì Ð Ð Ø ØÛ Ò ÒØ Ø Ö Ø Ò ØÛÓÖ Û Ö Ø Ö Ø ÖÑ Ò Ý Ö Ô ÝÑ ÒØ Ö ÕÙ Ö ØÛ Ò Ô Ö Ó ÒØ Ø º Ò Ø ÓÒ ½ Æ ØÛÓÖ G Ø Ô Ö N Eµ Û Ö N Ø Ó ÒÓ Ö ÔÖ ÒØ Ò ÒØ Ø Ò ÓÖ ÓÚ Ö Ò µ Ò Ø Ó E Ö ÔÖ ÒØ ÓÒØÖ Ø ØÛ Ò ØÛÓ ÒØ Ø ÖÓÑ Ð Ò Ö ØÓ ÓÖÖÓÛ Öº Ò Ø ÓÒ ¾ Û Ð P j1,j k ÕÙ Ò Ó ÒØ Ø (j 1,...,j k ) Ù Ø Ø Ø Ô Ö (j 1,j 2 ) (j 2,j 3 ) ººº (j k 1,j k ) E Ö Ó Ø Ò ØÛÓÖ º Ì Ð Ò Ø Ó Ø Û Ð P j1,j k Ú Ò Ý ½ Ë Ó u it ÓÒØ Ò ÙÒ ÖØ ÒØÝ ÓÙØ ÓÚ Ö Ò Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ Ò Ò Ò Ò Ö Ø Ó º ÀÓÛ Ú Ö Ø ØÖ Ú Ð ØÓ Ô Ö Ø ÐÝ Ò ÐÝÞ Ö Ø Ó º ÑÓ ÐÙ Ø Ðº ¾¼½ µ Ò Ð ÖÑ Ò Ò ÓÙÒ ¾¼½ µ ÑÔÐÝ Ø Ø Ó Ú Ò Ø Ú ÑÔ Ø ÓÒ Ö ØÙÖÒ º ÁÒ Ø Ô Ô Ö Ø Ó u it Ò Ú Ø Ö ÔÓ Ø Ú Ò Ò Ø Ú ÓÖ Ò Ò Ò ÒØ Ò Ù Ò ÓÒ Ë ÔÖ º
4 Ø ÒÙÑ Ö Ó k ÓÒØ Ò Ò Øº Ì Ñ Ò Ñ Ð Ð Ò Ø Ó Ø Û Ð P j1,j k ÓÖÖ ÔÓÒ ØÓ Ø Ø Ò D j1,j k º Ø Ò D ij ÒØÖÓ Ù Ò Ò Ø ÓÒ ¾ Ñ ÙÖ ØÛ Ò ØÛÓ ÒÓ i Ò j Ø Ø Ò ÓÖ ÒØ ØÝ Ó Ò ØÛÓÖ º Ì Ò ØÛÓÖ Ö Ø Ö Þ Ý ÒN N ÒÝ Ñ ØÖ Ü A Ø Ø ÓÒØ Ò ÐÐ Ò ÓÖÑ Ø ÓÒ ÓÙØ Ø Ò ØÛÓÖ º Ì ÒÝ Ñ ØÖ Ü A Ý Ò Ö ÒØ Ò Ò ÓÒÒ Ø Ò Ó Ø Ò ØÛÓÖ º ÌÓ ÐÐÙ ØÖ Ø Ø ÙÔÔÓ Ø Ø Ø Ø Ò D ij Ó Ø Û Ø Ø Ð Ò Ø Ó Ø ÓÒØ ÒÙÓÙ ÙÒØ ÓÒ y = f(x) Ò ÓÖ ÒÝ i Ò jº Ì Ò Ø Ø Ò D ij Ò Ò Ý l Ù ÒØ ÖÚ Ð Ó Û Ø xº ÁÒ Ø Ø Ø Ò D ij Ò ÔÔÖÓÜ Ñ Ø Ý Ö Ó ÒØ ÖÚ Ð D k,k = 1,...,l Û ÓÖ Ð Ö l ÕÙ Ú Ð ÒØ ØÓ l L D k 1 D k, ½µ k=1 L = lim l k=1 l D k 1 D k. ¾µ ÆÓÛ ÔÔÐÝ Ò Ø Ñ Ò Ú ÐÙ Ø ÓÖ Ñ Ø Ð Ò Ø L Ò ÛÖ ØØ Ò ˆ j ( ) dy 2 L = 1+ dx. µ dx i ÕÙ Ø ÓÒ µ ÑÔÐ Ø Ø Ø Ø Ò D ij Ò Ò Ø ÒÝ Ñ ØÖ ÜA ÙÐÐÝ Ö Ø Ö Þ ( 2 Ý Ø Ö Ú Ø Ú dy dx) Ø Ø ÓÙÐ ÐÙÐ Ø ØÓ Ó Ø Ò Ø ÓÒÒ Ø Ò Ñ ÙÖ Ó Ø Ò ØÛÓÖ º Ì Ö Ú Ø Ú Ò Ø Ñ Ø Ú ÓÖ Ø ÖÖÓÖ Ú Ö Ò ÓÑÔÓ Ø ÓÒ Û ÓÒ Ø ÒØ Û Ø Ø ÔÔÖÓ ¾ º Ï Ø Ò Ù ØÛÓ ØÝÔ Ó ÓÒÒ Ø ÓÒ ÖÓÑ ÓÙÖ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ ÔÔÖÓ ÑÔРݹ Ò ÓÖ ÑÔ Ò Ò º ÔÓ Ø Ú Û Ø Ö ÔÖ ÒØ Ò ÑÔÐ Ý Ò ÓÒÒ Ø ÓÒ Û Ö Ò Ø Ú Û Ø Ö ÔÖ ÒØ Ò ÑÔ Ò Ò ÓÒÒ Ø ÓÒº Ì Ò ÒØÓ ÓÙÒØ Ø Ø Ë ÔÖ ÔÖ Ö ¹ Ø Ô Ö Ú Ö Ó ÙÐØ ÚÓÖ Ð Ò Û Ö Ø Ú ÐÙ Ó Ø Ë ÔÖ Û Ð ÙÒ ÚÓÖ Ð Ò Û ÒÖ Ø Ú ÐÙ Ø Ù ÔÓ Ø Ú Û Ø A ij ÒØ Ý ÒØ Ø Ø Ø ÒÖ Ý Ø Ñ ÔÖÓ Ð ØÝ Ó ÙÐØ Û Ð ÒØ Ø Ó Ø Û Ø Ò Ø Ú Ú ÐÙ A ij Ö Ù Ø Ö Ó ÙÐØ Ò Ø Ò ØÛÓÖ º Ì Ò ÓÖÑ ÐÐÝ Ð Ò ØÓ ÕÙ Ø ÓÒ µ ÑÔÐÝ Ò Ø Ø Ø Û Ø Ò ØÓ Ó Ø Ò ØÛÓÖ Ò Ø ÓØ ÔÓ Ø Ú Ò Ò Ø Ú Ú ÐÙ º ÁÒ Ø Ò Ø Ò Ò Ö Ð Þ Ð Ò Ø Ñ ØÖ GL Ò GL = Ò Û sgn ÒÙÑ ÙÒØ ÓÒº ˆ j i sgn ( ) dy 1+ dx ( ) dy 2 dx, µ dx ¾ Ò ÐØ ÖÒ Ø Ú ÔÔÖÓ Ò ÐÐ Ó Ø Ðº ¾¼½¾µ ØÓ Ò Ò ÒÝ Ñ ØÖ Ü A ÖÓÑ Ö Ò Ö Ù Ð ØÝ Ø Ø Ò Û A ij = 1 i Ò j Ö ÓÒÒ Ø ÓÖ A ij = 0 ÓØ ÖÛ i,jº ÂÓÖ ÓÒ Ò Ò ¾¼¼ µ ÑÔ Þ Ø ÑÔÓÖØ Ò Ó ÔÓ Ø Ú Ò Ò Ø Ú ØÖ Ò Ö Ø Ò Ø Ë Ñ Ö Ø ¹ Ø Ý Ò ÔÓ Ø Ú ÓÖÖ Ð Ø ÓÒ ÖÓ Ë ÔÖ ÓÒØ ÓÒ Ø Ò Ò Ø Ú ÓÖÖ Ð Ø ÓÒ ÓÑÔ Ø Ø ÓÒ Ø º
5 Ò Ø ÓÒ ÁÒ Ö Ø Û Ø Ò ØÛÓÖ ÒÓ ØÛÓ Ö º Ì ÓÙع Ö δ out i = N j=1 A ji Ø ÒÙÑ Ö Ó ÓÙØ Ó Ò Ñ Ò Ø Ò ÖÓÑ ÒÓ i Ò Ø Ò¹ Ö δ in i = N j=1 A ij Ø ÒÙÑ Ö Ó ÒÓÑ Ò ØÓ ÒÓ º Ì ØÓØ Ð Ö Ó Ø ÒÓ Ò δ tot = δ in +δ out A ii º ÇÒ Ò ÒÝ Ñ ØÖ Ü A Ø Ñ Ø Ø Ö ØÖ ÙØ ÓÒ Ø ÔÖÓ Ð ØÝ ØÖ ÙØ ÓÒ Ó Ö ÖÓ ÒÓ Ò Ø ÓÚ Ö ÐÐ Ò ØÛÓÖ ÓÒÒ Ø Ò Ò Ø Ñ Ò Ó Ø Ö ØÖ ÙØ ÓÒ ÓÐÐÓÛ Ò ÓÐ Ò ÐÑ Þ ¾¼½ µµº Ì ÓÒÒ Ø Ò Ñ ÙÖ Ð Ø Ø ÙÒ Ö Ø Ò Ò Ó Ø ÑÔ Ò Ò Ò ÑÔÐ Ø ÓÒ Ñ Ò Ñ Ó Ý Ø Ñ Ö Ò ÑÓÖ Ø Ðº ÓÖ Ü ÑÔÐ ÖÓ Ù Ø¹ Ùع Ö Ð ³ Ò ØÛÓÖ À Ð Ò ¾¼¼ µ ÑÓ ÐÙ Ø Ðº ¾¼½ µµ Ñ Ý Ñ Ö Ò Ø Ó Ñ ÐÐ ÙÒ ÜÔ Ø Ó ØÓ Ø Ý Ø Ñ Ø ØÓÖ Ø Ø Ù ÐÓ ÓÖ Ñ ÒÝ ÒØ Ø º Ì Ö Ð ØÝ Ó Ò ØÛÓÖ Ö Ø Ö Þ Ý Ø ØÓØ Ð Þ Ó ÙÑÙÐ Ø Ñ ÐÐ Ò Ø Ú Ó Û ÒÖ Ò ØÛÓÖ ÓÒÒ Ø Ò Ò Ø Ý Ø Ñ ÙÐØ ÔÖÓ Ð ØÝ Û Ô Ò ÓÒÐÝ ÓÒ Ø ÓÐÙØ Ú ÐÙ Ó Ó º Ï Ô ÖÑ Ø Ð Ñ ÒØ Ó Ø ÒÝ Ñ ØÖ Ü A ij ØÓ Ò Ø Ú Ò ÓÒ ÕÙ ÒØÐÝ ÐÐÓÛ ÓÖ ÑÔ Ò Ò Ñ ÐÐ Ò Ø Ú Ó ØÖÓÒ ÐÝ Ø Ò Ø ÒØ ØÝ Û Ø Ý Ø Ñ Ö ÜÔÓ ÙÖ Ò Ó Ø Ý ÒÓØ Ö ÔÓ Ø Ú Ó º Ï Ù Ø ÔÔÖÓ ØÓ Ø Ø Ñ ¹Ú Ö Ð ØÝ Ó Ò ØÛÓÖ ÓÒÒ Ø Ò Û Ö ÕÙ Ö Ò Ö ÑÓÑ ÒØ Ó Ø Ö ØÖ ÙØ ÓÒº Ç Ò È ØØÓÒ ¾¼½ µ Ð Ø Ø ¹ Ò Ò Ó ÑÓ Ð Ò ÓÚ Ö Ø ÓÒ Ò Ó ÛÒ Ò Ë ÔÖ º ÁÒ Ø Ô Ô Ö Ø Ö Ø ÓÙÖ ÒØÖ Ð ÑÓÑ ÒØ Ó Ø Ö ØÖ ÙØ ÓÒ Ö Ö ØÐÝ Ú ÐÙ Ø ÖÓÑ Ò ÒÝ Ñ ØÖ Ü Aº Ï ÓÒ ØÖÙØ Ø Ñ Ò Ó Ø Ö ØÖ ÙØ ÓÒ Ø Ñ Ø ÒÓÖ Ò Ò Ó Ô ÐÐÓÚ Ö Û ÓÖÖ ÔÓÒ ØÓ Ø Ö Ø Ô ÐÐÓÚ Ö Ò Ü Ò ÓÒÚ Ý Ñ Ð Ö Ò ÓÖÑ Ø ÓÒº Ì Ú Ö Ò ÛÒ Ò ÙÖØÓ Ó Ò Ô ÐÐÓÚ Ö Ñ Ý ÙÒÓÚ Ö Ø Ò Ö ÒØ Ô Ó Ö º ËÙ Ø Ñ Ò Ö Ò ÓÔ Ò Ò Ú ÒÙ ÓÖ Ø ÓÒ ØÖÙØ ÓÒ Ó ÖÐÝ Û ÖÒ Ò Ñ ÙÖ Ó ÓÒØ ÓÒ Ò Ø ÔÖÓÔ Ø ÓÒ Ó Ý Ø Ñ Ö º ¾º¾ Û Ø Ö Ø Ò ØÛÓÖ Ó ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ï ÔÖÓÔÓ ØÓ Ñ ÙÖ ÓÒÒ Ø Ò Ð Ñ ÒØ A ij ÖÓÑ Ö Ó ØÓÖ Ð ÓÑÔÓ Ø ÓÒ ÓÖ Ú Ö ÓÙ ÒØ Ø Ù ØÓ ÜØ ÖÒ Ð Ó º Ì ØÓÖ Ð ÓÑÔÓ Ø ÓÒ ÜÔÐ Ò Ø Ö Ø ÓÒ Ó Ú Ö Ð i³ Ú Ö Ø ÓÒ Ø Ø Ñ t Ù ØÓ Ó Ò Ú Ö Ð jº ÓÐÐÓÛ Ò ÓÐ Ò ÐÑ Þ ¾¼½ µ Ý Ø Ñ Û ÓÒÒ Ø Ò Ø Ø Ñ t Ò ÙÑ Ó ÐÐ Ô ÖÛ ÓÒÒ Ø Ò Ñ ÙÖ ÜÐÙ Ò Ð ¹ÐÓÓÔ Ò Ò ØÛÓÖ º ÌÓ Ø ÒØÓ ÓÒ Ö Ø ÓÒ Ø ÔÓ Ð ØÝ Ó ÓÑÑÓÒ ØÓ Ø ØÖ Ò µ ØÛ Ò Ø Á ½µ Ë Ö Î ØÓÖ ÖÖÓÖ ÓÖÖ Ø ÓÒ ÅÓ Ð Î Åµ Ù k 1 Y t = αβ Y t 1 + Γ i Y t i +ε t, i=1 µ ÐØ ÖÒ Ø Ú ÓÒÒ Ø Ò Ñ ÙÖ Ù Ò ØÛÓÖ Ñ Ø Ö D max = max i,jd ij Ò Ð Ó Ù Ò Ø ØØ Ò º
6 Û Ö Y t = [Y 1,t ººº Y n,t ] Y t i = Y t i Y t i 1 Ò α,β,γ Ö Ø Ô Ö Ñ Ø Ö Ó Ø ÑÓ Ðº Ì Ö Ò Ó Ø Ñ ØÖ Ü Π = αβ Ø Ñ Ø Ý Ø ÂÓ Ò Ò Ø Ø Ò ÑÔÓ Ò Ø ØÖ Ò ÙÐ Ö Ö ØÖ Ø ÓÒ Ó È ÐÐ Ô ½ ½µº Ì Ô Ö Ñ Ø Ö Ó ÑÓ Ð µ Ö Ó Ø Ò Ý ÔÔÐÝ Ò ÇÄ˺ Î Å Ò µ Ò Ö ÔÖ ÒØ Î Ê µ Y t = k Φ i Y t i +ε t, i=1 µ Û Ø ÖÓ ¹ ÕÙ Ø ÓÒ Ö ØÖ Ø ÓÒ Φ 1 = αβ +Γ 1 +I n Ò Φ i = Γ i Γ i 1 i = 2,3,...,kº Ì Ö Ù ÓÖÑ Î Ê µ ÖÓÑ ÕÙ Ø ÓÒ µ Ò Ö ÛÖ ØØ Ò Ò Ø ÖÑ Ó ØÙÖ Ò Ò Ò Ø Ð ÓÒ Ø ÓÒ Ý ÔÔÐÝ Ò Ø ÑÓÚ Ò Ú Ö Ö ÔÖ ÒØ Ø ÓÒ Y t = Ò Ø Ð Ú ÐÙ + S i ε t i, Û Ö S j = Φ 1 Φ j 1 +Φ 2 S j ÓÖ j = 1,2,... Û Ø S 0 = I N Ò S j = 0 ÓÖ j < 0 Ò S j Ö Ù Ð Ò ÕÙ Ö ¹ ÙÑÑ Ð º ÒÝ Ò Ú Ù Ð Ð Ñ ÒØ Y j,t Ò Ö ÔÖ ÒØ Ý ÓÒØÖ ÙØ ÓÒ Ó ÐÐ Ú Ö Ð i=0 t 1 Y j,t = Ò Ø Ð Ú ÐÙ + S (j) i ε (j) t i, Û Ö ÔÖ ÒØ Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ó Ú Ö Ð j Ø Ø Ñ tº Á ÒÓÖ Ò Ò Ø Ð ÓÒ Ø ÓÒ ÕÙ Ø ÓÒ µ Ò Ö ÛÖ ØØ Ò Ò Ñ ØÖ Ü ÓÖÑ i=0 µ µ HD t+j = j 1 IRF i Υ t+j i = IRF i Υ t+j i + IRF i Υ t+j i, i=0 i=0 i=j µ Û Ö À Ñ Ö ÔÖÓ ÙØ Υ t+j i = [ε t+j i,...,ε t+j i ] Ø n n Ñ ØÖ Ü ÓÒØ Ò Ò Ö ¹ Ù Ð IRF i Ö ÒÓÒ¹ÓÖØ Ó ÓÒ Ð Þ ÓÒ ÙÒ Ø ÑÔÙÐ Ö ÔÓÒ Ñ ØÖ Ò HD t ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ñ ØÖ Ü Ø Ø Ñ tº Ï Ð ÓØ Ö Ò Ø ÓÒ Ó ÑÔÙÐ Ö ÔÓÒ ÒÐÙ Ò ÓÖØ Ó ¹ ÓÒ Ð Þ ÓÖ Ò Ö Ð Þ ÁÊ Ó ÃÓÓÔ Ø Ðº ½ µ Ò È Ö Ò Ò Ë Ò ½ µ Ö ÔÓ Ð Ø Ý Ó ÒÓØ Ô ÖÑ Ø Ò Ú Ù Ð ÓÑÔÓÒ ÒØ Ó HD t ØÓ ÙÔ ØÓ Y t, tº Ì Ø Ú ÔÖÓÔ ÖØÝ ÐÐÓÛ ÒØ ÖÔÖ Ø Ø ÓÒ Ó Ø Ð Ñ ÒØ Ó ØÓÖ Ð ÓÑÔÓ Ø ÓÒ HD t Ö Ó Ë ÔÖ Ñ ÙÖ Ò ÔÓ ÒØ ÓÒØÖ ÙØ Ò ØÓ Ø ØÓØ Ð Ý Ø Ñ ÙÐØ ÔÖÓ Ð Øݺ ÒÓØ Ö ÑÔÓÖØ ÒØ ÑÔÐ Ø ÓÒ Ó ÕÙ Ø ÓÒ µ Ø Ø Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒ HD t ÙÒØ ÓÒ Ó ÑÔÙÐ Ö ÔÓÒ Û Ø Ý Ö Ù Ð ε t ÓÒ Ø ÒØ Û Ø Ø Ú Û Ø Ø ÓÒÒ Ø¹ Ò Û Ø Ñ ÙÖ Ó Ó ÔÖ Ò Ø ÖÓÙ Ø Ò ØÛÓÖ º ÅÓÖ ÓÚ Ö Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒ HD t ÓÒØ Ò ØÛÓ Ö ÒØ Ø ÖÑ º Ì Ö Ö Ø Ø ÖÑ Ö ÔÖ ÒØ Ø ÜÔ Ø Ø ÓÒ Ó Y t+j Ú Ò Ò ÓÖÑ Ø ÓÒ Ú Ð Ð Ø Ø Ñ t Û Ø ÔÖÓ Ø ÓÒ Ó Y º Ì Ö Ø Ø ÖÑ ÓÒ Ø Ö Ø¹ Ò ÓÛ Ø Ö Ò ØÛ Ò Ø ØÙ Ð Ö Ò Ø ÔÖÓ Ø ÓÒ Ù ØÓ ÒÒÓÚ Ø ÓÒ Ù ÕÙ ÒØ ØÓ Ô Ö Ó tº ÁÒ Ô ÖØ ÙÐ Ö Ø ÓÛ Ø Ø Ø Ô ØÛ Ò Ò ØÙ Ð Ö Ò Ø ÔÖÓ Ø ÓÒ Ø ÙÑ Ó Ø Û Ø ÓÒØÖ ÙØ ÓÒ Ó Ø ÒÒÓÚ Ø ÓÒ ØÓ Ø ÓÒ Ø ÒØ Ø ÖÑ ÙÔÔÖ ÓÖ ÑÔÐ Øݺ ÁÒ Ø Ð Ú ÐÙ Û ÐÐ ÒÓÖ Ò Ø ÓÖØ ÓÑ Ò ÑÔ Ö Ð Ø ÓÒ ÓÐÐÓÛ Ò ÀÙ Ð Ò ÊÓ Ò ÓÒ ¾¼½¼µ Û Ø Ø ÓÒ ÕÙ Ò Ø Ø Ö Ø Ô ÖØ Ó Ø Ø Ó ÒÓØ ÔÖÓÚ ÑÔ Ö ÐÐÝ Ò ÐÝØ Ð ÓÑÔÓ Ø ÓÒ º
7 Ò Ú Ù Ð Ö º Ì Ö Ú Ð Ø ÝÒ Ñ ÔÖÓÔ ÖØ Ó Ø Ò ØÛÓÖ Ý Ø Ñ Ø Ø ÚÓÐÚ ÓÚ Ö Ø Ñ Ý Ú Ø Ò ÖÓÑ Ø ÐÓÒ ÖÙÒ Ø Ø º Ð Ñ ÒØ Ó Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ñ ØÖ Ü HD t,ij Ð Ý ÓÙÒ Ø ÓÒ Ó ÓÒÒ Ø Ò Ñ ÙÖ ÖÓÑ j ØÓ i ÒÓØ Ý c t i j º ÁØ ÓÒÚ Ò ÒØ ØÓ Ò ÐÝÞ ÓÒÒ Ø Ò Ñ ØÖ Ü C t = [HD t,ij ] Û Ö Ó ¹ ÓÒ Ð ÒØÖ Ñ ÙÖ Ô ÖÛ Ö Ø ÓÒÒ Ø Ò º ÁÒ Ò Ö Ð c t i j ct j i Ò¹ Ò ÓÙع Ö Ö ÒÓØ Ö ØÖ Ø ØÓ ÒØ Ðº Ì ÐÐÓÛ Ù ØÓ Ò Ò Ø Ô ÖÛ Ö Ø ÓÒ Ð ÓÒÒ Ø Ò c t ij = ct j i ct i j Û ÒÓØ Ö ØÖ Ø ØÓ ÔÓ Ø Ú º Ì Ò ÒØÓ ÓÙÒØ Ø Ø Ø ÙÑ Ó Ó ¹ ÓÒ Ð Ð Ñ ÒØ Ó Ø j¹ø ÖÓÛ Ó C t Ú Ø Ò Ö Ó Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒ ÓÑ Ò ÖÓÑ Ó Ö Ð Ø ØÓ ÓØ Ö Ú Ö Ð ØÓØ Ð Ö Ø ÓÒ Ð ÓÒÒ Ø Ò ÖÓÑ ÓØ Ö ØÓ i Ò c t i others = n j=1,j i HD t,ij, ½¼µ Ò ØÓØ Ð Ö Ø ÓÒ Ð ÓÒÒ Ø Ò ÖÓÑ j ØÓ ÓØ Ö c t others j = n i=1,j i HD t,ij. ½½µ ÙÖØ ÖÑÓÖ Ò Ø ØÓØ Ð Ö Ø ÓÒ Ð ÓÒÒ Ø Ò Ò ÐÙÐ Ø ÓÖ n Ú Ö Ð c t i = c t others i ct i others tº ÌÓ ÙÑÑ Ö Þ Ô ÖÛ Ö Ø ÓÒ Ð ÓÒÒ Ø Ò ÓÖ Ø ÑÔÐ T Û Ò c ij = 1 T T HD t,ij i j, ½¾µ t=1 Û Ò ÒØ ÖÔÖ Ø Ø Ø Ñ ÙÖ Ó ÓÒÒ Ø Ò ØÛ Ò ÒØ Ø i Ò jº Ì ØÓØ Ð Ó Ø Ó ¹ ÓÒ Ð ÒØÖ Ò C t Ò Ø Ö Ø Ô ÐÐÓÚ Ö Ò Ü Ñ ÙÖ Ò ØÓØ Ð ÓÑÔÐ Ø Ò Ø Ø Ñ t HDS t = 1 n (e C t e ØÖ (C t )). ½ µ Û Ö e Ø Ð Ø ÓÒ Ú ØÓÖ Ó ÓÒ º ¾º ÝÑÔØÓØ ÔÖÓÔ ÖØ Ó Ò Ô ÐÐÓÚ Ö Ò Ü Ì Ñ Ò Ó Ø Ú ÒÓÛ ØÓ ÔÖÓÚ ÜÔÖ ÓÒ ÓÖ Ø ÝÑÔØÓØ Ø Ò Ö ÖÖÓÖ Ó Ø Ò Ô ÐÐÓÚ Ö Ò Üº ÓÖ Ø ÔÙÖÔÓ ÙÔÔÓ γ Ú ØÓÖ Ó Ô Ö Ñ Ø Ö Ò ˆγ Ò Ø Ñ ØÓÖ Ù Ø Ø d T(ˆγ γ) N(0,Σγ ), ½ µ Û Ö d Ò ØÓ ÓÒÚ Ö Ò Ò ØÖ ÙØ ÓÒ Ò N(0,Σ γ ) ÒÓØ Ø ÑÙÐØ Ú Ö Ø ÒÓÖÑ Ð ØÖ ÙØ ÓÒº Ä Ø F(γ) = (F(γ 1 ),...,F(γ m )) Ö ÒØ Ð ÙÒØ ÓÒ Û Ø Ú ÐÙ Ò Ñ¹ Ñ Ò ÓÒ Ð ÙÐ Ò Ô Ò F i / γ = ( F i / γ j ) ÒÓÒÞ ÖÓ Ø γ ÓÖ i = 1,...,mº Ì Ò ÓÐÐÓÛ Ò Ä Ø ÔÓ Ð ½ ¼µ T[F(ˆγ) F(γ)] d N(0, F γ Σ γ F γ ). ½ µ ËØ Ø ÓÒÒ Ø Ò Ò Ð Ó Ò Ò ÜÔ Ø Ø ÓÒ Ó c t ij ÓÚ Ö Ø Û ÓÐ ÑÔÐ º
8 Ì Ò Ö Ð Ö ÙÐØ ÔÖÓÚ Ø ÓÖÑ Ó Ò ÝÑÔØÓØ ÓÚ Ö Ò Ñ ØÖ Ü ÓÖ Ø Ò Ô ÐÐÓÚ Ö Ò Ü Ö Ú ÖÓÑ Ø Ô ÖØ Ð Ö Ú Ø Ú Ó F Ò Ø Ú Ö Ò ÓÚ Ö Ò Ñ ØÖ Ü Σ γ º ÈÖÓÔÓ Ø ÓÒ ½ ËÙÔÔÓ T [ ˆη η ˆσ σ ] ( [ d Ση 0 N 0, 0 Σ σ ]). Ì Ò T Ú (ĤDi HD i ) d N(0,Ψ i Σ η Ψ i),i = 1,2,..., Û Ö Ψ i = Ú (HD i )/ η = i 1 m=0 R i 1 m G m, Ò Û G i = i 1 m=0 J(Φ ) i 1 m S m η = Ú (Φ 1,...,Φ k ) σ = Ú (Σ ε ) J = [I n 0...0] R i Ø ÓÒ Ð n 2 ¹Ú Ö Ø Ñ ØÖ Ü ÓÒØ Ò Ò Ö Ù Ð Ú (ε i,...,ε i ) ÓÒ Ø Ñ Ò ÓÒ Ð Ò Φ = Φ 1 Φ 2... Φ k 1 Φ k I n I n 0 0 º º ºº º º I n 0 À Ö Ú ÒÓØ Ø ÓÐÙÑÒ Ø Ò ÓÔ Ö ØÓÖ Ò Ú Ø ÓÖÖ ÔÓÒ Ò ÓÔ Ö ØÓÖ Ø Ø Ø ÓÒÐÝ Ø Ð Ñ ÒØ ÓÒ Ò ÐÓÛ Ø ÓÒ Ð Ò Ø ÃÖÓÒ Ö ÔÖÓ Ùغ. ÈÖÓÓ ÔÔ Ò Ü ÈÖÓÔÓ Ø ÓÒ ½ ÓÛ Ø Ø Ò ÝÑÔØÓØ Ú Ö Ò ¹ÓÚ Ö Ò Ñ ØÖ Ü Ó Ø ØÓÖ Ð ÓÑÔÓ ¹ Ø ÓÒ HD i Ö Ø Ö Þ Ý Ö Ù Ð Ô Ö Ñ Ø Ö Ó Ø ÑÓ Ð Ò ÓÒ ÙÒ Ø ÑÔÙÐ Ö ÔÓÒ º Å ØÖ Ü Σ η Ò Ø Ñ Ø Σ η = (ZZ /T) 1 Σ ε Z t = [Y t,...,y t k+1 ] Z = (Z 0,...,Z T 1 ) ÓÖ Î Ê ÑÓ Ð Ò [ Σ co Y 1 Y η = T 1 Y 1 X XY 1 X X ] 1 Σ co ε ÓÖ Î Å º ÁÒ Ø Y 1 = [Y 0,...,Y T 1 ] Ò X t 1 = [ Y t 1,..., Y t k+1 ] Ò Σ co ε Ú Ö Ò ¹ÓÚ Ö Ò Ñ ØÖ Ü ÖÓÑ Î Å º º Ä Ø ÔÓ Ð ¾¼¼ µµº ÁÒ Ø ÓÖØ ÓÑ Ò ÑÔ Ö Ð ØÙ Ý Ë ÔÖ Ö Á ½µ Ö Ò ÓÖ Ø Ö ÓÒ Ø Î Ê Û Ø ÖÓ ÕÙ Ø ÓÒ Ö ØÖ Ø ÓÒ Ò Ò ÕÙ Ø ÓÒ µ Ó Ò Ò Ñ Ö ÑÓ Ðº Ì ÝÑÔØÓØ Ú Ö Ò ÖÓÑ ÈÖÓÔÓ Ø ÓÒ ½ Ó ÒÓØ Ó ØÓ Þ ÖÓ ÙØ ÓÒÚ Ö ØÓ Ø Ö Ô Ø Ú ÐÓÒ ÖÙÒ Ú ÐÙ Û Ø Ø ÑÔÐ Þ º Ò ÑÔÐ Ø ÓÒÚ Ò ÒØ ÙÑÔØ ÓÒ Ó ÕÙ Ø ÓÒ µ Ø Ø Y t Þ ÖÓ Ñ Òº Ì Ö ÙÐØ Ó ÈÖÓÔÓ Ø ÓÒ ½ Ö Ñ Ò Ú Ð ÒÓÒÞ ÖÓ Ñ Ò Ø ÖÑ ÔÓÐÝÒÓÑ Ð ÓÖ ÓÒ Ð ÓÑÔÓÒ ÒØ Ö ÑÓÚ ÔÖ ÓÖ ØÓ Ø Ñ Ø Ò Ø Î Ê Ô Ö Ñ Ø Ö º ÕÙ Ú Ð ÒØÐÝ ÔÓÐÝÒÓÑ Ð ÓÖ ÓÒ Ð ØÖ Ò Ò ÒÐÙ Ò Ø ÑÓ Ð µ Ò Ø Ñ Ø Ó ÒØÐÝ Û Ø ÓØ Ö Ó ÒØ Û Ø ÓÙØ Ø Ò ÈÖÓÔÓ Ø ÓÒ ½º Ì ÓÐÐÓÛ ÖÓÑ Ø Ø Ø Ø Ø ÝÑÔØÓØ Ú Ö Ò Ò ÈÖÓÔÓ Ø ÓÒ ½ ÓÒÐÝ Ô Ò ÓÒ Ô Ö Ñ Ø Ö Φ i Ò Ú Ö Ò ¹ÓÚ Ö Ò Ñ ØÖ Ü Σ η º
9 Ï Ð ÈÖÓÔÓ Ø ÓÒ ½ Ò Ø Ø ÓÖ Ò Ú Ù Ð ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ó ÒØ Ñ ØÖ ÓÒ Ò ÜØ Ò Ø Ö ÙÐØ ÓÖ Ø Û Ö Ø Ð Ñ ÒØ Ó ĤD i Ò ĤD j i j Ö ÒÓØ Ò Ô Ò ÒØ ÝÑÔØÓØ ÐÐݺ Á Ð Ñ ÒØ Ó ØÛÓ ÓÖ ÑÓÖ HD i Ñ ØÖ Ö ÒÐÙ Ò Ø ÒÙÐÐ ÝÔÓØ Ø Ó ÒØ ØÖ ÙØ ÓÒ Ó ÐÐ Ø Ñ ØÖ Ò Ø Ñ Ø Ù Ò ÈÖÓÔÓ Ø ÓÒ ½º ÁÒ Ô ÖØ ÙÐ Ö Ø ÓÚ Ö Ò Ñ ØÖ Ü Ó Ø Ó ÒØ ÝÑÔØÓØ ØÖ ÙØ ÓÒ Ó Ú (ĤD i,ĥd j) Ò Û Ú (HD i,hd j ) Ú (HD i,hd j ) Σ η η, η [ Ú (HD i,hd j ) Ú (HDi )/ η = η Ú (HD j )/ η ÆÓÛ Ø Ö ÙÐØ Ó ÈÖÓÔÓ Ø ÓÒ ½ Ò Ù ØÓ Ó Ø Ò Ø ÝÑÔØÓØ ØÖ ÙØ ÓÒ Ó Ø ÒØ ÖÓÒÒ Ø Ò Ò Ü ÓÒ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ º ]. ÈÖÓÔÓ Ø ÓÒ ¾ ËÙÔÔÓ Q i = (Ψ i Σ η Ψ i /T) Ú ØÓÖ Ó Ô Ö Ñ Ø Ö Ú Ö Ò Ò HDSi Ô ÐÐÓÚ Ö Ò Ü Ò ÖÓÑ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ò ½ µº Ì Ò T( ĤDS i HDS i ) d N(0,(e W i e ØÖ (W i ))/n),i = 1,2,..., Û Ö W i = ÙÒÚ (Q i ) Ò ÓÔ Ö ØÓÖ ÙÒÚ Ø ÒÚ Ö Ó Ø Ú ÓÔ Ö ØÓÖ Ù Ø Ø W i = ÙÒÚ (Ú (W i ))º ½ µ ÈÖÓÓ ÔÔ Ò Ü ÈÖÓÔÓ Ø ÓÒ ¾ Ô ÖÑ Ø Ø Ø Ñ Ø ÓÒ Ó Ø Ø Ò Ö ÖÖÓÖ Ó HDS i ÕÙ Ö ÖÓÓØ Ó Ú Ö Ò Ò Ò ½ µº Ò ÑÔÓÖØ ÒØ ÙÑÔØ ÓÒ ÓÖ ÈÖÓÔÓ Ø ÓÒ ¾ Ø Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒ ÙÒ ÕÙ ØÖ Ò ÓÖÑ Ø ÓÒ Ó Ø º ÅÓÖ ÓÚ Ö ÒÓÒ¹ ÓÒ Ð Ð Ñ ÒØ Ó ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ñ ØÖ Ü HD j Ö ÓÖØ Ó ÓÒ Ð Ý ÓÒ ØÖÙØ ÓÒ Û ÐÐÓÛ Ù ØÓ Ó Ø Ò Ø ÓÒ Ò ÓÙÒ ÓÖ Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ô ÐÐÓÚ Ö Ò Ü Ý Ø Ò Ú Ö ÖÓ Ø ÒÓÒ¹ ÓÒ Ð Ð Ñ ÒØ Ó W i º Ñ Ð Ö ÔÔÖÓ Ò ÒÓØ ÔÔÐ ØÓ Ø Ô ÐÐÓÚ Ö Ò Ü ÔÔÖÓÔÖ Ø ÒÓÖ¹ Ñ Ð Þ Ø ÓÒ Ö ØÖ Ø ÓÒ Ø Ø Ò ÙÖ ÓÖ Ø ÖÖÓÖ Ú Ö Ò ÓÑÔÓÒ ÒØ ÙÑ ÙÔ ØÓ ½ Ö Ö ÕÙ Ö º Ì Ö ØÖ Ø ÓÒ Ñ Ø Ö Ú Ø ÓÒ Ó Ø ÝÑÔØÓØ ØÖ ÙØ ÓÒ Ó Ú Ö Ò ÓÑÔÓ Ø ÓÒ ÓÑÔÓÒ ÒØ ÙÐغ Ì Ù Ø ÝÑÔØÓØ ØÖ ÙØ ÓÒ Ó Ø Ò Ü Ò ÒÓØ Ó Ø Ò Ò Ø Ù Ù Ð Û Ý ÓÖ ØØ Ò ÙÔ ÓÒ Ò ÒØ ÖÚ Ð º Ø ÅÓ Ð Ò Ø ÒØ ÖÓÒÒ Ø ÓÒ ØÛ Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ ÑÔ Ö Ý Ø Ú Ð Ð Øݺ ÇÒ Ø ÓÒ Ò Ñ ÒÝ Ó Ø Ø ÓÖ Ø Ð Ö Ñ ÛÓÖ Ö ÜÔÖ Ò Ø ÖÑ Ó ÒØ Ö¹ ÒØ ØÝ ÓÛ º ÀÓÛ Ú Ö Ø Ø Ö Ü Ò ÐÝ ÙÐØ ØÓ Ó Ø Ò Ô ÖØ ÙÐ ÖÐÝ ÓÙØ Ø ÓÑÑ Ö ÐÐÝ Ú Ð Ð Ø Ø ÓÓ Ü ÑÔÐ Ø Íà ÒØ Ö Ò Ò ØÛÓÖ Ò Ö Ø Ø Ðº ¾¼½ µ Û Ó Ù Ø Ú Ð Ð ØÓ Ø Ò Ó Ò Ð Ò º ÇÒ Ø ÓØ Ö Ò Ø Ö ØÖ Ò Ó Ð Ø Ö ØÙÖ Ø Ø Ø Ú ÒØ Ó Ñ Ö Ø¹ Ø ÔÖÓÜ ØÓ Ú ÐÓÔ Ò ÙÒ Ö Ø Ò Ò Ó Ø ÒØ ÖÓÒ¹ Ò Ø Ò Ó Ò ØÛÓÖ Ò ÓÖ Ü ÑÔÐ ÐÐ Ó Ø Ðº ¾¼½¾µ Ò Å ÖØÓÒ Ø Ðº ¾¼½ µº Ê ÒØ
10 ÛÓÖ Ý Ú Ò Ä ÙÖ Ø Ðº ¾¼½ µ Ò Ø Ø ÒØ ÖÓÒÒ Ø Ò Ò ØÛÓÖ ÓÒ Ñ Ö Ø Ø ÔÖÓ Ù Ú ÐÙ Ð Ò ÓÖÑ Ø ÓÒ Ø Ø ÒÓØ Ó Ö Ý ÐØ ÖÒ Ø Ú ÔÔÖÓ º Ì ÛÓÖ Ò Ø Ô Ô Ö Ö Û ÓÒ Ø Ñ Ö Ø¹ Ø ØÖ Ø ÓÒ Ò Ø Ð Ø Ö ØÙÖ º Ì Ð ½ ËÓÚ Ö Ò ÒÐÙ Ò Ë ÑÔÐ Ø º ¹ Ú ÐÓÔ ¹ Ñ Ö Ò ¹ ÖÓÒØ Ö Ñ Ö Ø ÓÖ Ò ØÓ Ø ÅË Á Ð Ø ÓÒº ÙÖÓÔ Ä Ø Ò Ñ Ö ÙÐ Ö µ Ù ØÖ Ð µ Ö ÒØ Ò µ Þ Ê ÔÙ Ð µ Ò µ Ö Þ Ð µ ÒÑ Ö µ ÁÒ ÓÒ µ Ð µ ÆÓÖÛ Ý µ Â Ô Ò µ ÓÐÓÑ µ ÈÓÐ Ò µ Å Ð Ý µ Å Ü Ó µ ËÛ Ò µ È Ð ÔÔ Ò µ È Ò Ñ µ ÊÙ µ ËÓÙØ ÃÓÖ µ È ÖÙ µ ÌÙÖ Ý µ Ì Ð Ò µ Î Ò ÞÙ Ð µ Í Ö Ò µ Î ØÒ Ñ µ Ö ÙÖÓ ÓÒ ÆÓÖØ Ñ Ö Á Ö Ð µ Ð ÙÑ µ ÍË µ ÅÓÖÓÓ µ ÒÐ Ò µ ËÓÙØ Ö µ Ö Ò µ É Ø Ö µ ÖÑ ÒÝ µ ÁÖ Ð Ò µ ÁØ ÐÝ µ Æ Ø ÖÐ Ò µ ÈÓÖØÙ Ð µ ËÔ Ò µ Ì Ø Ø ÓÒ Ø Ó ÐÝ Ú ¹Ý Ö Ë ÔÖ ÓÖ ¼ ÓÚ Ö Ò Ò Ø ÓÒ Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ Ð Ø Ò Ì Ð ½ Ò ¾º Ú ¹Ý Ö Ë ÓÒØÖ Ø Ö Ø ÑÓ Ø ÓÑÑÓÒÐÝ Ù Ò ØÖ Ø Ò Ø Ð Ò Ö Ø ÑÓ Ø Ð ÕÙ Ù Ò È ÐØÓÒ Ò ¾¼½ µ È Ò Ò Ë Ò Ð ØÓÒ ¾¼¼ µ Ã Ð Ò Ø ÓÛ ¾¼½¾µµº Ì Ø Ö ÓÙÖ ÖÓÑ Å Ö Ø Ò ÖÙÒ ÓÖ Ø Ô Ö Ó Â ÒÙ ÖÝ ½ ¾¼¼ ØÓ ÆÓÚ Ñ Ö ¾½ ¾¼½ º ÔÓØ ÒØ ÐÐÝ ½½ ¾ (= 67!»65!) Ð Ò º Ì ÑÔÐ ½¼ ÒÓ Ò Ì ÑÔÐ ÓÒØ Ò Ø Ö Ö ÒØ Ô È ½ Ö ÔÖ ÒØ Ø ÒÓÒ¹Ö Ô Ö Ó ÖÓÑ Â ÒÙ ÖÝ ½ ¾¼¼ ØÓ Ë ÔØ Ñ Ö ½ ¾¼¼ º Ì ØÝÔ Ð Ó Ø Ò ÓÒÚ ÒØ ÓÒ Ù Ò Ð Ø Ö ØÙÖ ØÓ Ô Ö Ø Ø ÔÖ ¹Ö Ò Ö Ô Ö Ó Ø Ö Ú Û Ó Ø ÜØ ÒØ Ò Ø Ð Ø Ö ØÙÖ Ò ÙÒ Ý Ø Ðº ¾¼½ µº È ¾ Ö ÔÖ ÒØ Ø Ô Ö Ó ÖÓÑ Ë ÔØ Ñ Ö ½ ¾¼¼ ØÓ Å Ö ½ ¾¼½¼ ÓÒ Ø ÒØ Û Ø Ø ÐÓ Ð Ò Ò Ð Ö µ Ò Ô Ö Ó ÓÐÐÓÛ Ò º Ì Ò Ó Å Ö ¾¼½¼ Ö ÔÖ ÒØ Ø Ô Ö Ó ÔÖ ÓÖ ØÓ Û Ø Ö Ø Ö Ñ Ö Ø Ð Ò ÔÖ Ð ¾¼½¼º È ÖÓÑ ÔÖ Ð ½ ¾¼½¼ ØÓ ÆÓÚ Ñ Ö ¾½ ¾¼½ Ö ÔÖ ÒØ Ø Ô Ö Ó Ó Ø Ö Ò ÙÖÓÔ Ò ÓÚ Ö Ò Ø Ö º ËÙÑÑ ÖÝ Ø Ø Ø Ö ÔÓÖØ Ò Ì Ð ÓÛ Ò ÒÖ Ò ÔÖ Ñ Ò ÓÖ ÇÙÖ Ø Ò Ò ÆÓÚ Ñ Ö ¾¼½ ÓÖ Ø Ò Ø Ð Ö Ø Ó Ø Ô Ô Öº ÇÒ ÙÔ Ø Ò Ø Ø Ø Û ÓÙÒ Ø Ø Ø Ö Û Ö Ò ÒØ Ò Ò Ð Ø Ö Ø Ù ØÓ Ø Ó ¹ Ö Ò Ø Ò Ø ÑÔÐ Ñ ÒØ Ø ÓÒ Ó Ø Ó¹ ÐÐ ÎÓÐ Ö ÖÙÐ Û Ø Ò Û¹ Ù Ò Ó ÍË ÓÐÐ Ö ÒÓÑ Ò Ø Ë ÓÖ Ñ ÒÝ Ó Ø Ò Ø ØÙØ ÓÒ Ò ÓÙÖ ÑÔÐ º ½¼
11 ÑÓ Ø ÖÓÙÔ Ó Ò Ø ØÙØ ÓÒ Ò ÓÚ Ö Ò Ö Ø Ò Ø Ô Ö Ú ÒÖ Ò Ö ÙÖ Ò Ø ØÙÖ ÙÐ ÒØ Ô Ö Ó Ò ÒØ ÖÒ Ø ÓÒ Ð Ø Ñ Ö Ø º Ë ÛÒ Ò È ¾ Ò Ö ÓØ ÐÓÛ Ö Ø Ò Ò Ô ½ Ü ÔØ Ò ÙÖÓÔ Ô ¾µ Û ÑÔÐ Ð ÝÑÑ ØÖݺ ÅÓÖ ÓÚ Ö ÙÖØÓ ÑÙ Ö ÓÖ Ø ÓÖ ÑÓ Ø Ó Ø ÒØ Ø º ËÓÑ Ó Ø Ö ÙÐØ Ñ Ø Ö Ø Ø ÓÒ Ø Ò Ý Ø ÙØ ÓÖ Ø Ø Ø Û Ö ÑÓÖ Ö Ú Ò Ø ÍË Ø Ò Ò ÙÖÓÔ ÓÖ Ó Ò ¾¼½ µµº Ë ÔÖ Û Ö ÓÙÒ ØÓ ÒÓÒ¹ Ø Ø ÓÒ ÖÝ Á ½µ Û Ø Ñ Ü ÑÙÑ Ó ÓÒ ÙÒ Ø ÖÓÓØ ÓÖ Ò ØÓ ÃÈËË Ò Ø Ø º Ì Ð ¾ Ò Ò Ð Ò Ø ØÙØ ÓÒ ÖÓÙÔ Ý ÖÓ ØÝÔ º ËÁ ¹ ÐÓ Ð ËÝ Ø Ñ ÐÐÝ ÁÑÔÓÖØ ÒØ Ò º Ò Ò Ò Ð ÁÒ ÙÖ Ò Ù Ø ² Æ Û Ð ÇÅ Ç ÄÌ ÄØ Ñ ÖÒ ÜÔÖ Ó ÂÓ Ò Ö Ô ÓÖÔ ÓÒ ÆºÎº ÖÐ Ý ÔÐ ËÁ µ Å Á ÁÒº Ñ Ö Ò ÁÒØÐ Ô ÁÒ ÆÈ È Ö ËÁ µ Æ ØÐ ÊÙÖ Ð ÍØ Ð ÓÓÔ ÐÐ Ø Ø ÓÖÔ Ô ÇÒ ÒÐ ÓÖÔ ÙÐ ÓÖÔ ÓÒ ÓÖÔ Ø ÖÓÙÔ ÁÒ ËÁ µ ÇÊÁ ÓÖÔ ÙÖ Þ ÓÒ Ò Ö Ð ØÖÝÛ ÀÓÑ ÄÒ Ò Ð Ô ÓÖÔ ÀÍ ÇÊÈ ÃÓÓ Ñ Ò ÓÐ Ñ Ò Ë Ô ÁÒ Æ ÒÐ ÓÖÔ ÓÑÑ ÖÞ Ò ËÁ µ ÅÓÖ Ò ËØ ÒÐ Ý Ä Ð ² Ò Ô ÈÄ ÙØ ËÁ µ Ë ÊË ÊÇ Í Ã Å Á ÁÒ ÓÖÔ À Ò Ò ÌÓÝÓØ ÅØÖ Ö ÓÖÔ Å ØÄ ÁÒ ÀË ÔÐ ËÁ µ ËÛ Ö È ÄØ ÅÙÒ Ê ÁÆ Æ Î ËÁ µ ÇÐ ÅÙØ ÔÐ ÃÓÖ Ú Ë Ó ÓÖÔ Å ÖÖ ÐÐ ÄÝÒ ² Ó Å Ø Ù ËÙÑ ØÓÑÓ ÁÒ Å ÞÙ Ó ÓÖÔÓÖ Ø ËÁ µ ËÓÑÔÓ Â Ô Ò ÁÒ ÁÒ Å ÕÙ Ö ÄØ À ÊÌ ÇÊ ÁÆ ÁÆ Æ ØÐ Ù Ø ÄØ ÄÓ Û ÓÖÔ ÇÚ Ö Ò Ê Ó Ò Æ ÖÐ Ò ÊÓÝ Ð Ó ËÓØÐ Ò ËÁ µ Ê ÓÒ ÄØ ËÓ Ø Ò Ö Ð ËÁ µ ËØ ÖØ Ö ËÁ µ ËÙÑ ØÓÑÓ Å Ø Ù ËÁ µ Í Ë ËÁ µ Ï ÐÐ Ö Ó ² Ó ËÁ µ Ï ØÔ ÓÖÔ ÁÒÚ ØÑ ÒØ Û Ë Ô ÓÑ Ö Ö ÆÓÑÙÖ Ë Ê Ð Ø Ø ÇÈ ÇÔ Ö ÄØ È Ô À ÑÑ Ö ÓÒ ÈÄ ÀÓÒ ÓÒ Ä Ó Å Ø Ù Ø Ø Ó Ë ÑÓÒ ÈÔØÝ Ô Ä È Ë ÑÓÒ ÈÔØÝ Ô ÁÒ ½½
12 Ì Ð ËÙÑÑ ÖÝ Ø Ø Ø Ö Ö ÔÓÖØ ÓÖ ÐÐ ÓÚ Ö Ò Ë ÔÖ Ø Ù Ò Ø Ô Ô Öº Ì Ð Ø Ô Ö Ö Ô Ø Ú ÐÝ ÓÒ Ø ÒØ Û Ø Ø ÔÖ ¹ Ø Ò Ø ÙÖÓÔ Ò Ø Ö º Ç º Å Ò ËØ Ú Ë ÛÒ ÃÙÖØÓ È ½ ¼½»¼½»¾¼¼ ¹ ½»¼»¾¼¼ Ò ½ ¼º ¾ ¼º º¾¾ ¾ º½ ½ Ò Ò Ð ½ ¼º ¾ ½º º¾ ½ ½º ÁÒ ÙÖ Ò ½ ¼º ½ ½º½½ ½¼º ½ ½ º¾ ¼ ÁÒÚ ØÑ ÒØ ½ ½º¼½¾ ½º ¼¾ º ¼ ½ º Ê Ð Ø Ø ½ ¼º ¼º ½ ¾º ¼ ½½º ¼ Ä Ø Ò Ñ Ö ½ º ¾ º¼ ¼¾ º ¾ ¾ º ¼ ½ ½º¼ ½º ¼ ½º º½ ¼ ÙÖÓ ÓÒ ½ ¼º¼ ¼º¼ ¾º ½½º ÙÖÓÔ ½ ¼º ¼ ¾ ½º ¾½½ ¾º ½ ½ º ½ Ö ½ ¼º ¼ ¼º ¾¼ ¾º ¼ ½½º ÆÓÖØ Ñ Ö ½ ¼º¼¾ ¾ ¼º¼ ½½ ¾º ¾ ½½º¼¾ È ¾ ½»¼»¾¼¼ ¹ ½»¼»¾¼½¼ Ò ¼ ½º ¼ ½º¾ ¾º½ º Ò Ò Ð ¼ ½¾º ½ ¾º ½ º º ÁÒ ÙÖ Ò ¼ º ¼ º½¼¾ ¾º ½ º¾¼ ½ ÁÒÚ ØÑ ÒØ ¼ ½º ¼ ½º½ ½½ ½º¼ ¾½ ¾º ½ Ê Ð Ø Ø ¼ ¾º ¼ ¼ ¾º ¾ ½º ¾ º½¾¾ Ä Ø Ò Ñ Ö ¼ º ½ º ½ ¾º¾ ½ º ½ ¼ ¾º¼½ ½º ½º º¼ ÙÖÓ ÓÒ ¼ ¼º ¾ ¼ ¼º ½º º ¼ ÙÖÓÔ ¼ º º º ¾¼º¾ Ö ¼ ½º ¾ ¼º ¼ ½º º ½ ÆÓÖØ Ñ Ö ¼ ¼º ½ ¼º½ ½º½ º È ¼½»¼»¾¼½¼ ¹ ¾½»½¼»¾¼½ Ò ½ ½º ½ ¼º ½º º Ò Ò Ð ½ º ½¼º¾½½ ¾º¼ º ¼ ÁÒ ÙÖ Ò ½ ½º ½ ¾º½ º ¾¼º¼ ÁÒÚ ØÑ ÒØ ½ ½º ½º¼ ¾ ¼º ¾º¾¾ Ê Ð Ø Ø ½ ½º½¼ ¼º ¼º ¼ ½ ¾º ½ ¾ Ä Ø Ò Ñ Ö ½ º º º½½¼ ½ º ¼ ½ ½º ¾ ¼º ¾ ½º º½ ¼ ÙÖÓ ÓÒ ½ ¾º ¾ ¾º ½º ¾ º½ ÙÖÓÔ ½ ½º ¾ ½º ¾¾¼ ¾º¾ ¼ º ¼ Ö ½ ½º ¼ ¼º ¼ ¼º ¾º ¼¼¼ ÆÓÖØ Ñ Ö ½ ¼º ¼ ¼º¼ ¼½ ¹¼º¾ ½ ¾º ¾ ½¾
13 º½ ÑÔ Ö Ð Ö ÙÐØ ËØ Ø ÓÒÒ Ø Ò ÙÖ ½ ÓÛ Ø Ú Ö ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ó Ø Ó ÓÒØÖ ÙØ Ò ØÓ Ó ÖÚ Ë ÔÖ ÓÖ Ó Ø ÓÚ Ö Ò Ò Ø ÓÒ Ò Ø ÑÔÐ º Ì Ø Ø Ú ÖØ Ð Ü Ò Ø Ø Ö Ô ÒØ Ù Ò ÓÙÒØÖÝ Ò Ø ÓÖ ÞÓÒØ Ð Ü Ú Ø ÓÒØÖ ÙØ Ò Ó Ñ ÙÖ Ø ÑÔÐ Ú Ö Ó Ø Ó Ó ÖÓ Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒº Ä Ø Ö ÓÐÓÙÖ Ò Ø ÔÓ Ø Ú ØÖ Ò Ñ ÓÒ ¹ Ø Ø Ø Ó ÒÖ Ø Ë ÔÖ Ò Ø Ö Ô ÒØ Ñ Ö Øº Ö Ö ÓÐÓÙÖ Ò Ø Ò Ø Ú ØÖ Ò Ñ ÓÒ ¹ Ø Ó Ö Ø Ë ÔÖ Ò Ø Ö Ô ÒØ Ñ Ö Øº Ì Ø Ð ÔÖ Ñ Ö ÐÝ ÔÔÖÓÜ Ñ Ø ÐÝ Ø Ú Ö Ó Þ ÖÓ Ö Ô ÒØ»ØÖ Ò Ñ ÓÒ Ó ¹ ÓÒ Ú Ö Ø Ø Ö Ð Ö ÐÝ Ò ÐÐ ÓÙØ ÓÚ Ö Ø ÑÔÐ º ARGENTINA AUSTRALIA BELGIUM BULGARIA BRAZIL CHILE CHINA COLOMBIA CZECH GERMANY DENMARK FINLAND FRANCE INDONESIA IRELAND ISRAEL ITALY JAPAN KOREA MALAYS MEXICO MOROCCO NETHERLANDS NORWAY PANAMA PERU PHILIPPINES POLAND PORTUGAL QATAR RUSSIA SOUTH AFRICA SPAIN SWEDEN THAILAND TURKEY UKRAINE US VENEZUELA VIETNAM ARGENTINA AUSTRALIA BELGIUM BULGARIA BRAZIL CHILE CHINA COLOMBIA CZECH GERMANY DENMARK FINLAND FRANCE INDONESIA IRELAND ISRAEL ITALY JAPAN KOREA MALAYS MEXICO MOROCCO NETHERLANDS NORWAY PANAMA PERU PHILIPPINES POLAND PORTUGAL QATAR RUSSIA SOUTH AFRICA SPAIN SWEDEN THAILAND TURKEY UKRAINE US VENEZUELA VIETNAM ÙÖ ½ À Ø Ñ Ô ÓÖ ÓÚ Ö Ò º Ø ÖÓÑ ÓÐÙÑÒ ØÓ ÖÓÛ Ö ÔÖ ÒØ Ú Ö Ó ØÓÖ Ð ÓÑÔÓ Ø ÓÒ ÓÚ Ö Ø Û ÓÐ ÑÔÐ º Ö ÓÐÓÖ ÓÛ Ò Ø Ú ÓÒØÖ ÙØ ÓÒ ØÓ Ë ÔÖ Ö Ø ÓÐÓÖ ¹ ÔÓ Ø Ú ÓÒØÖ ÙØ ÓÒ º ½
14 ÁØ Ö Ø Ð ØÓ Ö ÒØ Ø Ò Ø Ú Ò¹ Ó ÖÓÑ ÔÓ Ø Ú ÓÙع Ó Ò Ø ÙÖ ¹ ÖÓ Ø ÖÓÛ Ú Ø ÓÙÖ Ò Ò Ó Ò¹ Ó ØÓ Ø Ø Ö Ø Ð Ø Ò Ô ÖØ ÙÐ Ö ÖÓÛ ÓÛÒ Ø ÓÐÙÑÒ Ú Ø Ø Ó ÓÙع Ó ÓÙÖ ÖÓÑ Ø ÓÙÒØÖÝ Ð Ø ÓÖ Ø Ø Ô ÖØ ÙÐ Ö ÓÐÙÑÒ ØÓ Ó Ø ÔÓØ ÒØ Ð Ö Ô ÒØ Ð Ø ÓÛÒ Ø ÓÐÙÑÒº Ê Ò ÖÓ ÖÓÛ Ø Ø Ö Ö Û ÓÙÒØÖ Û ÓÛ ÓÑ Ú Ö ØÝ Ò Ø Ö ÓÙÖ Ó Ó º ÓÒ Ö Ø ÖÓÛ Ð ÐÐ Ö ÒØ Ò Û Ü Ø ÓØ ÑÔÐ Ý Ò Ò ÑÔ Ò Ò Ó ÓÙÖ ÖÓÑ Ø Ô ÖØÒ Ö º Ë Ó ÖÓÑ È ÖÙ Ò ÓÐÙÑ Ö ØÖÓÒ ÐÝ Ò Ø Ú ¹ Ö Ò Ø Ë ÔÖ ÓÖ Ö ÒØ Ò º ÀÓÛ Ú Ö Ó ÖÓÑ Î Ò ÞÙ Ð ÅÓÖÓÓ Ò ÌÙÖ Ý ÓÒ Ú Ö ÒÖ Ø Ë ÔÖ Ñ ÙÑ ÓÖ Ö ÒØ Ò º ÁÒ Ò ØÛÓÖ Ö Ñ ÛÓÖ Ó Ø Ö Ø ÓÒ ÐÐÝ Ö ÔÖ ÒØ Ò Ò¹ Ó ÖÓÑ Ø ÓÒØÖ ÙØ Ò Ñ Ö Ø ÙØ Ø Ý Ö Ò ØÓ Û Ø Ö Ø Ý ÑÔÐ Ý ÓÖ ÑÔ Ò Ø Ø Ó Ø Ó Ó ÓÒ Ö ÒØ Ò º ÇØ Ö ÒØ Ö Ø Ò Ü ÑÔÐ Ó Ñ Ö Ø Û ÔÐ Ý Û Ò Ø Ö ÓÙÖ Ó Ó ÖÓ Ø ÖÓÛ µ Ö ÁÖ Ð Ò ÈÓÖØÙ Ð ËÔ Ò ÁØ ÐÝ Í Ö Ò Ò Î Ò ÞÙ Ð Ø Ø Ø Ý ÒÐÙ Ñ Ñ Ö Ó Ø Ó¹ ÐÐ ÁÁÈË ÖÓÙÔ ÜÔ Ö Ò Ú Ð ÙÒÖ Ø ÓÖ Û Ö ÐÓ Ø Ò ËÓÙØ Ñ Ö º ÙÖ ¾ ÓÛ Ø Ñ Ø Ñ Ô ÓÖ Ø Ò Ò Ð Ò Ø ØÙØ ÓÒ Ò ØÛÓÖ º Ê Ò ÖÓ ÖÓÛ Ø ÔÔ Ö ÒØ Ø Ø Á Á Å Á Å Ò ØÓ ÓÑ ÜØ ÒØ ËÀ Ö Ú Ú Ö Ø Ó Ó º ÄÓÓ Ò Ø Ø ÓÐÙÑÒ ÓÖ Ø ÓÙÖ Ó Ó Û Ò Ø Ø Á Å Á Ò Å Ö ÒÓØ Ø ÒØÐÝ Ö ÒØ ØÓ ÓØ Ö ÓÑÔ Ò º Ì Ò Ø ØÙØ ÓÒ Ö Ù Ø ØÓ Ú Ö Ó ÙØ Ó ÒÓØ Ñ Ø Ó Û ØÖÓÒ ÐÝ ÑÔ Ø Ò ÓÒ Û Ý ÓÖ Ø ÓØ Öº Ì Ù Ò ÙÖ Ö Ö Ô Ö ÓÖÑ Ò Ø ÖÓÐ Ó ÓÖ Ò Ò ÑÓÓØ Ò Ó ÓÑ Ò ÖÓÑ ÓØ Ö Ò Ø ØÙØ ÓÒ Ò Ñ ØØ Ò Ó Û Ø Ð ØØÐ Ò Ø ÓÒ ÓØ Ö Ò Ò Ð Ò Ø ØÙØ ÓÒ º ÖÓÑ Ø ÔÓ ÒØ Ó Ú Û Ø Ò ÙÖ Ö Ö Ø Ò ØÓ Ø Ð Ø Ò Ò Ð Ý Ø Ñ Ö Ø Ö Ø Ò ÔÓØ ÒØ ÐÐÝ ÖÙÔØ Øº Ì Ö ÙÐØ ÙÔÔÓÖØ Ö ÙÑ ÒØ Ø Ø Ø ÖÓÐ Ó Ò ÙÖ Ö Ò Ø Ý Ý Ø Ñ Ø ÒØ ØÓ Ø Ø Ó Ö Ø Ö Ø Ò Ò Ø ØÙØ ÓÒ Ò Ê Ö ÓÒ ¾¼½ µº Ì Ö Ö Ð Ó ØÛÓ Ø ÒØÐÝ Ö ÒØ Ú ÖØ Ð Ð Ò Ò ÙÖ ¾ ÖÓÑ ÇÅ ÓÑ Ö Ö Ô Ø Ð ÁÒÓÖÔÓÖ Ø µ Ò ËÏÁ ÀÓÒ ÃÓÒ ÓÒ ÐÓÑ Ö Ø º ÓØ Ó Ø ÖÑ Ö Ú ÐÝ Ò¹ Ú Ø Ò Ø ØÖ Ò ÔÓÖØ Ò Ø Ò Ò Ò ØÓÖº Ì Ö ÙÐØ Ø Ø ØÖ Ò ÔÓÖØ Ò Ò ÑÔÓÖØ ÒØ Ò ÔÖ Ò Ó ÒØ Ö Ø Ò ÐÝ Ô Ö ÐÐ Ð Ý Ø Ö ÒØ Ò Ò Ó È Ö Ò Ò Ò ¾¼½ µ Ø Ø Ø ØÖ Ò ÔÓÖØ Ò Û Ö ÓÙ Ò ØÓÖ Ó Ø ÍË ÓÒÓÑÝ ÖÓÙØ Ò ÐÝ Ø ÑÓ Ø ÑÔÓÖØ ÒØ ØÓÖ Ó Ø ÍË ÓÒÓÑ Ò ØÛÓÖ º ÌÓ ÐÐÙ ØÖ Ø ÓÛ Ø ØÖ ÙØ ÓÒ Ó Ó Ø Ò ÓÚ Ö Ø ÑÔÐ Ô Ö Ó ÙÖ ÔÖ ÒØ Ø ØÓ Ö Ñ Ó Ø Þ Ó Ø Ó Ò Ó Ø Ø Ö Ô Ó Ø ÑÔÐ ÔÖ ¹ Ò ÙÖÓÔ Ò Ø Ö º Ì ØÓÔ Ô Ò Ð ÓÛ Ø ØÖ ÙØ ÓÒ Ó Ø Ó Ò Ø Ò Ò Ð ÓÑÔ Ò ÓÑÔÓÒ ÒØ Ó Ø Ò ØÛÓÖ Ò Ø ÐÓÛ Ö Ô Ò Ð Ø ØÖ ÙØ ÓÒ ÓÖ Ø ÓÚ Ö Ò º ÁÒ Ø ÔÖ ¹Ö Ô Ö Ó Ø ÑÓ Ó ¼ ÔÖÓÒÓÙÒ Ò Ø Ð Ö Ö Ð Ø Ú ÐÝ Ñ ÐÐ ÓÖ ÓØ Ô Ò Ð º ÙÖ Ò Ø Ò ÙÖÓÔ Ò Ø Ö Û Ø Ø Ø ØÖ ÙØ ÓÒ ÑÓÚ ØÓ Ø Ö Ø ¹ Ø Ø Ø Ö Ö ÑÓÖ ÔÓ Ø Ú ÑÔÐ Ý Ò µ Ó ÔÖ ÒØ Ø Ò ÔÖ ¹Ö º Ì ØÖ ÙØ ÓÒ ÑÓÖ Ð ÔØÓ ÙÖØ ÑÔÐÝ Ò Ö Ø Ö ÔÖÓÔÓÖØ ÓÒ Ó Ð Ö Ö Ò Ó º Ì Å Á Ò Å Ö Ø Ò ÙÖ Ò Ò Ò Ò Ð ÖÑ Ó Ø Ñ ÓÑÔ ÒÝ Å Á µ Ò Ö ÔÖ ÒØ Ø Ð Ö Ø ÓÒ Ò ÙÖ Ö Ò Ø Ñ Ö ØºÌ ÙÐ ÓÖÔÓÖ Ø ÓÒ Á µ Â Ô Ò Ò Ò Ð ÖÚ ÔÖÓÚ Öº ½
15 Ò Ò Ö¹ÓÖ Ö ÑÓÑ ÒØ Ó ÓÙÖ Ó Ö ÓÒ Ø ÒØ Û Ø Ø Ò Ò Ò ÖÝ Ø Ðº ¾¼½¼µ Ø Ø ÓÒØ ÓÒ Ò Ö Ö Ú ÒØ Ò Ö¹ÓÖ Ö ÑÓÑ ÒØ Ó Ö ØÙÖÒ Ò ÚÓÐ Ø Ð Ø º ACE ACO AEG AIF AIG ALL ANZ AOC ASS AXP BAC BNP BOM C CB CCR CIT CMZ CNA COF DAI DB DE EOP GE GS HAM HAN HIG HKL HSB INT KDB LGE LTR MBI MBC MER MET MIT MIZ MQB MUN MWD NAB NOM NRU OCB OLD ORI RAB RBO RES SAF SHC SOC SPG SPG STA SUM SWI TAI TOY UBS WFC WST YAS ACE ACO AEG AIF AIG ALL ANZ AOC ASS AXP BAC BNP BOM C CB CCR CIT CMZ CNA COF DAI DB DE EOP GE GS HAM HAN HIG HKL HSB INT KDB LGE LTR MBI MBC MER MET MIT MIZ MQB MUN MWD NAB NOM NRU OCB OLD ORI RAB RBO RES SAF SHC SOC SPG SPG STA SUM SWI TAI TOY UBS WFC WST YAS ÙÖ ¾ À Ø Ñ Ô ÓÖ Ò Ò Ð ÓÑÔ Ò º Ø ÖÓÑ ÓÐÙÑÒ ØÓ ÖÓÛ Ö ÔÖ ÒØ Ú Ö Ó ØÓÖ Ð ÓÑÔÓ Ø ÓÒ ÓÚ Ö Ø Û ÓÐ ÑÔÐ º Ö ÓÐÓÖ ÓÛ Ò Ø Ú ÓÒØÖ ÙØ ÓÒ ØÓ Ë ÔÖ Ö Ø ÓÐÓÖ ¹ ÔÓ Ø Ú ÓÒØÖ ÙØ ÓÒ º ½
16 Financial companies Phase 1 Phase 2 Phase Sovereigns Phase 1 Phase 2 Phase ÙÖ Ò Ø ÓÖ Ô ÔÖ ¹ Ò ÙÖÓÔ Ò Ø Ö µº Ô Ö ÔÖ ÒØ Ò Ì Ð º Ø Ó Ø º¾ ÝÒ Ñ ÓÒÒ Ø Ò Û ÐÐ Ø Ú Ö Ø Ù Ò Ø ÔÖ Ú ÓÙ Ø ÓÒ Û Ð Ó ÓÑÔ Ð Ô ÐÐÓÚ Ö Ò ÓÒ Ø Ñ Ø Ó ÓÐÓ Ý Û Ø ½¼ Ý ÓÖ Ø Ô Ö Ó µ Ò Ù Ò Ø ÔÖÓÔÓ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ñ Ø Ó º Ì Ö ÓÛÒ Ò ÙÖ º Ì Ò ØÙÖ Ó Ø ÓÒ ØÖÙØ ÓÒ Ó Ø Ò Ñ Ò Ø Ø Ø Ð Ö ÕÙ Ø Ö ÒØ ¹ Ø À Ñ Ø Ó Ö Ø ÒØ ÖÔÖ Ø Ø ÓÒ Ó Ø Ú Ö Þ Ó Ø Ô ÐÐÓÚ Ö ØÓ Ë ÔÖ ÖÓÑ ÐÐ ÓÙÖ Ò Ø Ý Ø Ñ Ò Ø Ò Ò Ø Ø Ø ØÝÔ ÐÐÝ ÕÙ Ø Ñ ÐÐ Ò Ó Ø Ò Ò Ò ÒØ Ò Ø ÖÐÝ Ô ÖØ Ó Ø Ò ÐÝ Ú Ø ± ÖÖÓÖ ÓÒ Ò Ò º Ì Ò Ü Ð Ö Ö ÐÛ Ý ÔÓ Ø Ú µ Ú ÐÙ Ù ØÓ ÒÓÖÑ Ð Þ Ø ÓÒ ØÛ Ò ¼ Ò ½ Ù Ò Ø ÔÖ Ú ÓÙ Ø ÓÒ º Ì Ô ÐÐÓÚ Ö Ò Ü ÒÖ Ö Ñ Ø ÐÐÝ Ò Ñ ¹¾¼¼ ÔÖÓ ÐÝ Ó Ø Û Ø Ø Ú ÒØ Ó Ö¹ËØ ÖÒ Ò ÙÒ Ò Ø Ñ Ð Ó Ø Ø Ý Öº Ì À ÑÓ Ð Ô ÙÔ Ø Ø Ø ÔÓ ÒØ ÙØ Ô ÙÔ ½
17 ÑÙ ÑÓÖ Ù Ø ÒØ ÐÐÝ Ø Ø ÐÓ Ö ØÓ Ø ØÖ Ó Ø Û Ø Ä Ñ Ò ÖÓ ÓÐÐ Ô Ò Ø Ù ÕÙ ÒØ ÔÖÓ Ð Ñ Ò Ø Ö Ñ Ò Ö Ó Ø Ý Ø Ñº ÁÒØ Ö Ø Ò ÐÝ Ø Ô ÐÐÓÚ Ö Ò Ü Ó ÒÓØ ÐÐ Ö Ñ Ø ÐÐÝ Û Ø Ø ÒØÖÓ ÙØ ÓÒ Ó Ì ÊÈ ÓÖ Ø Æ Ê Ø Ò Ó Ø Ò Ò Ó Ø ÍË Ö ÓÒ Ó Ø Ò Ù Ð Û Ö Ò Ø Ð Ø Ö ØÙÖ ÙÒ Ý Ø Ðº ¾¼¼ µ ÓÖ Ö Ú Ûµ ÙØ Ö Ñ Ò Ð Ú Ø º Ì À Ò Ü ÓÛ Ú Ö ÓÛ ÓÑ Ö ÙØ ÓÒ Ò Ø Ø Ó Ø Ô ÐÐÓÚ Ö ÓÒ Ë ÔÖ ÔÓ Ø Ø ÙØ Ö ÙÖ Ò Ó ÔÓ Ø Ú Ø ÖÓÙÒ Ø Ô Ö Ó Ó ÙÒ ÖØ ÒØÝ ÙÖÖÓÙÒ Ò Ø ÙØÙÖ Ó Ö Ò Ð Ø ¾¼¼ ¹ ÖÐÝ ¾¼½¼ Ò Ø Ö ¹ Ñ Ö Ò Ó ÙÒ ÖØ ÒØÝ Ò ÖÓÙÒ ÙÖÓÔ Ò Ø Ñ Ö Ø Ò ¾¼½½ Ò ¾¼½¾º ÙÖ ÔÖ ÒØ Ø À Ë Ò ÓÖ Ø Ò Ò Ð Ò Ø ØÙØ ÓÒ Ò Ø ÓÚ Ö Ò Ô Ö Ø ÐÝ ÜØÖ Ø ÖÓÑ Ø ÓÑ Ò Ò ØÛÓÖ º ÁØ ÑÑ Ø ÐÝ ÔÔ Ö ÒØ Ø Ø Ø Ô ÐÐÓÚ Ö Ø ÖÓÑ Ø ØÛÓ ÓÙÖ Ú Ö Ñ Ø ÐÐÝ Ö ÒØ Ø Ñ Ô Ø º ÈÖ ÓÖ ØÓ Ø ÖÓÑ Ñ ¹¾¼¼ Ò Ò Ð Ò Ø ØÙØ ÓÒ Û Ö Ò Ø Ú Ò Ò Û Ý Û Ö Ù Ø Ú Ö Ë ÔÖ º ÇÒÐÝ Û Ò Ø Ñ Û Ðй Ø Ð Ø ÓÒØÖ ÙØ ÓÒ Ó Ò Ò Ð Ò Ø ØÙØ ÓÒ Ô Ò Ú Ò Ø Ò Ø Ö Ø Ø ÓÒØÖ ÙØ ÓÒ Û Ö Ó ÖÚ Ò ¾¼¼ Ö Ø Ö Ø Ò ÖÓÙÒ Ø Ø Ñ Ó Ø ÓÐÐ Ô Ó Ä Ñ Ò ÖÓ º Ì ÖÖÓÖ Ò ÓÛÒ Ò Ø Ö Ñ Û Ò Ù Ø ÒØ ÐÐÝ ÖÓÙÒ ÖÐÝ ¾¼½¼ Û Ò Ø Ö Ö Ù ÕÙ ÒØ ÁÅ ÔÖÓ Ö Ñ Ò ÙÖÓÔ Ò Ø ÔÖÓ Ð Ñ ÙÒ ÓÐ º ÙÖ Ò Ø Ô Ö Ó ÖÓÑ ¾¼¼ Ø ÓÒØÖ ÙØ ÓÒ ØÓ Ô ÐÐÓÚ Ö Ò Ø Ë Ñ Ö Ø ÖÓÑ ÓÚ Ö Ò Ò ÙÒ ÖÖ Ò ÐÝ ÔÓ Ø Ú Ò ÓÒ Ú Ö ÑÓÖ Ø Ò Ø Ñ Ö Ø Ö Ø Ò ÙÖ Ò Ø º Ì Ô ØØ ÖÒ Ö ÖÓÑ Ó Ø Ò Ò ÐÑ Þ ¾¼½ µ Û Ó ÓÙÒ Ø Ø ÓÒÒ Ø Ò Ó Ø ÐÓ Ð ÓÚ Ö Ò Ñ Ö Ø Ý Ø Ò Ó ¾¼½ Ö ØÙÖÒ ØÓ Ø Ñ Ð Ú Ð Ø Û ÓÖ Ø º 1 Diebold-Yilmaz spillover index Jan-2005 Jan-2006 Jan-2007 Jan-2008 Jan-2009 Jan-2010 Jan-2011 Jan-2012 Jan Spillover index based on historical decompositions Jan-2005 Jan-2006 Jan-2007 Jan-2008 Jan-2009 Jan-2010 Jan-2011 Jan-2012 Jan-2013 ÙÖ Ò À Ë Ò Ø Ñ Ø ÖÓÑ ÕÙ Ø ÓÒ ½ µ ÓÖ ½¼ ÔÖ º Ë Ö Ö ÔÖ ÒØ ± ÓÒ Ò ÒØ ÖÚ Ð º ½
18 0.2 Financial companies Jan-2005 Jan-2006 Jan-2007 Jan-2008 Jan-2009 Jan-2010 Jan-2011 Jan-2012 Jan Sovereigns Jan-2005 Jan-2006 Jan-2007 Jan-2008 Jan-2009 Jan-2010 Jan-2011 Jan-2012 Jan-2013 ÙÖ À Ë Ò ÓÖ Ò Ò Ð Ò Ø ØÙØ ÓÒ Ò ËÓÚ Ö Ò º Ë Ö Ö ÔÖ ÒØ ± ÓÒ Ò ÒØ ÖÚ Ð º º ÓÒØÖ ÙØ ÓÒ Ý ÓÙÖ ØÝÔ Ø ÓÒØÖ ÙØ ÓÒ Ó Ó Ø ÓÙÖ Ó Ó Ö Ø Ú Ò ÓÙÖ ÔÔÖÓ Û Ò ÓÑÔ Ð Ù ¹ Ö Û ÐÐÙ ØÖ Ø Ø ÓÒØÖ ÙØ ÓÒ Ó Ô ÖØ ÙÐ Ö ÖÓÙÔ Ò ÓÒ Ø ÔÖ º ÓÖ Ó Ø ØÝÔ Ó Ò Ò Ð Ò Ø ØÙØ ÓÒ ÙÖ ÓÛ Ø Ö À Ë Ô ÐÐÓÚ Ö Ò ÓØ Ö Ô ÒØ Ó Ó Ð Ø Ò Ô Ò Ð µ Ò ÔÖ Ö Ó Ó Ö Ø Ò Ô Ò Ð µº ÁØ Ù ÙÐ ØÓ ÔÓ ÒØ ÓÙØ Ø Ø Ø Ð ÓÖ Ù ¹ ÙÖ Ö ÓÑ Ø Ñ Ù Ø ÒØ ÐÐݺ ½¼ Ì Ñ Ò Ö ÙÐØ ÖÓÑ ÙÖ Ø Ø Ø Ð Ö Ø ÔÖ Ö Ó Ó Ø Ò ØÓÔ Ö Ø Ò Ô Ò Ðµº ÇØ Ö ÔÖ Ö Ú Ù Ø ÒØ ÐÐÝ Ñ ÐÐ Ö ÑÔ Ø ÓÒ Ø Ö Ø Ó Ø Ý Ø Ñº Ö Ô ÒØ ÓÛ Ú Ö Ø Ò Ó ÒÓØ Ö Ú Ö Ø Ð Ó ÑÔ Ø ÖÓÑ ÓØ Ö ØÓÔ Ð Ø Ò Ô Ò Ðµº Ï Ø Ø Ü ÔØ ÓÒ Ó Ø Ò Ò Ð Ò Ø ØÙØ ÓÒ Ø ÓÖÝ ÐÐ ÓØ Ö ØÝÔ ÔÖ Ó ÑÓÖ Ø Ò Ø Ý Ö Ú Ø Ñº Ï Ò Ö Ú Ò Ó Ó Ø Ð Ø Ò Ô Ò Ð Ó ÙÖ ÓÛ Ø Ø Ø Ó Ö Ú ÑÔÐ ÚÓÐ Ø Ð ØÝ Ø Ø Û Ö ÔÓ Ø Ú Ø µ ÙÖ Ò Ø ¾¼¼ ¹ ¾¼¼ Ö ÐØ ÓÙ Ø ÓÒ Ò Ò Ó ÒÓØ Ò Ø Ò Ò Ò ÐÐ º ÀÓÛ Ú Ö Ò Ø ÔÖ Ò Ó Ó ÙÖ Ò Ø Ö Ó ¾¼¼ ¹¾¼¼ Ò Ø ÖÓÙ ØÓ ¾¼½¼ Ø Ú ÖÝ ÔÔ Ö ÒØ Ø Ø Ø ÓÖÝ Ó Ò Ø ØÙØ ÓÒ Ö ÒØ ÖÓÐ º Ò Û Ö ÓÒØÖ ÙØ Ò ØÓ ÑÔ Ò Ò Ó Ò Ø Ý Ø Ñ ÔÖ ÓÖ ØÓ Ø ÙØ Ö Ô ÐÝ Ñ ÑÔÐ Ö Ò Ú Ð Ö ÐÝ Ö Ñ Ò Ø Ø Û Ý Ò º ÀÓÛ Ú Ö Ò ÙÖ Ö ÑÔ Ò Ò Ø ÙÖ Ò ¾¼¼ ¹¾¼½½ Ø Ô Ö Ó ÔÖ ÓÖ ØÓ Ø Ð Ö Ø ½¼ Í Ò Ø Ñ Ð Ò ÐÝØ ÐÐÝ ÒØÖ Ø Ð º ½
19 ÖÙÔØ ÓÒ Ò ÙÖÓÔ Ò Ñ Ö Ø º Ì Ø Ø Ò ÙÖ Ö Û Ö Ø Ø Ø Ñ Ö Ú Ò ÑÔÐ Ý Ò Ó Ò ØÖ ÙØ Ò ÑÔ Ò Ò ÓÒ º Ì ÓØ Ö Ô ÖØ ÙÐ ÖÐÝ ÒØ Ö Ø Ò ÔÖ Ö Ø ÓÖÝ Ö Ð Ò Ù ØÖÝ ÓØØÓÑ Ö Ø Ô Ò Ðµ Û Ö Ò Ù ØÖÝ Ó Û Ö ÑÔ Ò Ò Ó ÔÖ ÓÖ ØÓ Ø º ÙÖ Ò Ø Ù Ð ÙÔ ØÓ Ø Ò Ø Ò Ø Ð Ø Ò Ù ØÖÝ Ó Û Ö ÑÔÐ Ý Ò ÙØ Ø Û Ö Ú Ö ÙÖ Ò Ð Ø ¾¼¼ ÓÒ Ø ÒØ Û Ø Ø Ö Ò Ó Ð Ò ØÛ Ò Ø Ö Ð ÓÒÓÑÝ Ò Ò Ò Ð ØÓÖ ÒÓØ Ò ÙÒ Ý Ø Ðº ¾¼½ µ Ù ØÓ Ø ÒØÖÓ ÙØ ÓÒ Ó Ì ÊÈ Ò Ö Ù Ó Á º ÙÖ ÁÒØ ÖÓÒÒ Ø Ò ØÛ Ò Ö ÒØ ÖÓÙÔ Ó Ò Ò Ð Ò Ø ØÙØ ÓÒ Û Ø ± ÓÒ ¹ Ò ÒØ ÖÚ Ð Ø Ñ Ø ÖÓÑ ÕÙ Ø ÓÒ ½ µº ½
20 ÙÖ ÁÒØ ÖÓÒÒ Ø Ò ØÛ Ò Ö ÒØ ÖÓÙÔ Ó Ò Ò Ð Ò Ø ØÙØ ÓÒ Û Ø ± ÓÒ ¹ Ò ÒØ ÖÚ Ð Ø Ñ Ø ÖÓÑ ÕÙ Ø ÓÒ ½ µº ÙÖÓÞÓÒ ÒÓØ ÔÖ ÒØ Ø Ö Ô Ø Ú À Ë Ò Ü ÒÓØ Ò ÓÖÑ Ø Ú Ò ÐÓ ØÓ Þ ÖÓº ÙÖ Ö ÔÖ ÒØ Ø Ó Ö Ô Ð Ò Ù Ò Ó Ö Ú Ò Ò ÔÖ Ò Ó Ó º Ô Ò Ð Ö ÔÖ ÒØ Ø Ú Ö Ø Ó Ó ÖÓÑ Ø ÔÖ Ò Ö ÓÒ ØÓ Ø Ö Ô ÒØ Ö ÓÒ Ø Ð Ø Ó ÓÖ ÓÑÔ Ö ÓÒ Ú Ò Ø Ø Ø Ö Ö ÓÖ Ü ÑÔÐ Ñ ÒÝ ÑÓÖ Ù Ö Ò ÙÖÓÔ Ø Ò ÆÓÖØ Ñ Ö ÓÖ Ü ÑÔÐ µº ÙÖÓÔ Ø Ö Ô ÒØ Ó Ø Ð Ö Ø ÑÔ Ø Ó Ó ÐØ ÓÙ Ø Û Ö ÜÔ Ö Ò ÙÖ Ò Ø ÔÖÓ Ð Ñ Ó Ø Ô Ö Ó Ó Ð Ø ¾¼¼ ÙÖ Ò Ø ÔÓ Ø¹Ä Ñ Ò ÖÓ ØÙÖÑÓ Ð Ò ÙÖ Ò Ø Ö Ñ Ò Ö Ó Ø ÑÔÐ Ø Ø ÖÓÑ Ø Ö Ø Ó Ø ÛÓÖÐ Ñ Ö Ø Û Ö ÕÙ Ø Ù Ù ½½ º Ì Ð Ö Ø Ò ÐÝØ Ð Ö Ò Ø Ø ÔÖ ÓÖ ØÓ ¾¼¼ Ø Ñ ÓÖ ØÝ Ó Ø Ö Ú Ó ÑÔ Ò ÙÖÓÔ Ò Ë ÔÖ Û Ð Ø Ø Ö ¾¼¼ ½½ ÆÓØ Ø Ø ¼± Ó Ò Ò Ò ÓÑ ÖÓÑ Ò Ò ÙÖÓÔ Ò ÓÒÐÝ ¾¼± Ò Ø ÍË Ñ ÓÖØ Ø Ðº ¾¼½ µº ¾¼
21 Ø Ý Ð Ö ÐÝ ÑÔÐ Ø Ñ ÐØ ÓÙ Ò Ò Ø Ö Ö Ø Ø Ø Ø Ø ÐÐÝ Ò Òصº Ì ÔÖ Ò Ó Ó ÖÓÑ ÙÖÓÔ ÓÛ Ö ÒØ Ô ØÙÖ ÙÖ Ò Ø Ô Ö Ó ÔÖ ÓÖ ØÓ Ñ ¹ ¾¼½¼ ÙÖÓÔ Ð Ö ÐÝ ÔÖ Ø Û Ù Ù Ë ÔÖ Ð Û Ö Ø Ø Ø Ý ÐÑ Ô Ö ÔØ ÓÒ Ó Ö Ð Û Ö º ÀÓÛ Ú Ö ÙÖ Ò Ø Ô Ö Ó Ó ¾¼½½ Ô ÖØ ÙÐ ÖÐÝ Ø Ý ÓÒØÖ ÙØ Ò Ò ÒØÐݵ ØÓ ÑÔÐ Ý Ò Ó º Ì Ö ÓÒ Û ÔÖ ÓÒ Ú Ö Ø Ð Ö Ø ÓÒØÖ ÙØ ÓÒ Û Ö ÙÖ Ò ¾¼¼ ¹¾¼¼ ÓÒØÖ ÙØ ØÓ Ø ÑÔÐ Ø ÓÒ Ó ÔÖ Ò Ë Ñ Ö Ø Ù Ø ÒØ ÐÐÝ Ò Ò ÒØÐݺ ÓÖ Ø Ñ ÓÖ ØÝ Ó Ø Ö Ø Ó Ø Ô Ö Ó Ñ ÒÐÝ ÓÒØÖ ÙØ ÑÔ Ò Ò Ø ÓÒ ÓØ Ö Ñ Ö Ø ¹ ÐØ ÓÙ Ø Û Ö ÐÑÓ Ø ÙÒ ÓÖÑÐÝ Ò Ò Òغ ÁÒ ÓÒØÖ Ø Û ÒÓØ Ö Ô ÒØ Ó Ð Ö ÑÔ Ò Ò ÓÖ ÑÔÐ Ý Ò Ø ÖÓÑ ÒÝÛ Ö Ò Ø Ö Ø Ó Ñ Ö Ø ¹ ØÝ Ò Û Ø Ò ÐÝ Ø Ø Ò Ñ Ö Ø Ð Ö ÐÝ Ò ¹ÔÓ ÒØ ÒÓ ÓÖ Ò Ô Ö Ø Ñ Ö Ø ÖÓÑ ÓØ Ö Ñ Ö Ø º Ä Ø Ò Ñ Ö Ò Ö Ú Ö Ð Ø Ú ÐÝ Ð Ö Ö Ò Ò Òص Ø ÖÓÑ Ø Ö Ø Ó Ø ÛÓÖÐ Û Û Ø ÙÖÓÔ Û Ö ÑÔ Ò Ò ÔÖ ÓÖ ØÓ Ø ¾¼¼ ¹¼ Ö Ò Û Ø Ð Ö Ø ÑÔÐ Ý Ò ÑÔ Ø ÙÖ Ò Ø Ö Ô Ö Ó Ò Ø Ò Ö Ù Ø Ø Ö Ø Öº Ì ÔÖÓ Ð Ñ Ð Ö ÓÖ Ö º ÆÓÖØ Ñ Ö Û Û Ø Ø ÒØÖ Ó Ø Ò Ó Ø Ò Ö Ö Ø Ò Ö Ø Ò Ñ Ö Ø Ò Ø Ð Ø Ö ØÙÖ Ö Ú Ð Ø Ø Ö Ô ÒØ Ø Ú ÖÝ Ñ ÐÐ Ø ÖÓÑ ÓØ Ö Ö ÓÒ ÓÒ Ø ÓÛÒ Ë ÔÖ º Ì Ö Ð Ø Ô Ö Ó Ø Ø Ø Ó Ø ØÙÖÑÓ Ð ÖÓÙÒ Ä Ñ Ò ÖÓ Û Ö Ø ÑÔ Ø Ó ØÖ Ò Ñ ÓÒ ÖÓÑ ÓØ Ö Ñ Ö Ø Û Ø Ø Ø ÐÐÝ ÑÔÐ Ý Ò ÆÓÖØ Ñ Ö Ò Ë ÔÖ Ñ Ò Ú Ò Ø Ø Ø Ö Ø Ö Ø Ø Ø Ú Ö Ò Ò Òص Ø ÔÓ Ø Ú º ÁÒ ÓÒØÖ Ø Ø Ú Ö Ø ÔÖ ÖÓÑ ÆÓÖØ Ñ Ö Ö Ø Ø Ø ÐÐÝ Ò ÒØ Ò Ö Ð Ø Ú ÐÝ Ð Ö º ÈÖ ÓÖ ØÓ ¾¼¼ Ø ØÖ Ò Ñ ÓÒ ÓÖ Ò Ø Ò Ò Ø ÍË Ò ÑÔ Ò Ò Ë ÔÖ Ò Ñ ¹¾¼¼ º Ì Ö Ø Ú Ò Ó ÑÔÐ Ý Ò Ó ÓÙÖ Ò Ð Ø ¾¼¼ Ò ÖÐÝ ¾¼¼ Ò ÖÓÑ Ø Ø Ö ÕÙ ÖØ Ö Ó ¾¼¼ ÙÒØ Ð ÔÔÖÓÜ Ñ Ø ÐÝ Ø Ô Ö Ó Ó Ø Û Ø Ø Ò Ó Ø Æ Ê Ø Ö ÓÒ Ò Ñ ¾¼¼ Ø Ø Ó ÍË ÓÖ Ò Ø Ó Ð ÖÐÝ ÑÔÐ Ý Ë ÔÖ Ñ Ð Û Ö º Ö ÒØ ÖÑ ÓÒ Ó Ò ÙØÖ Ð ØÓ ÑÔ Ò Ò Ó ÔÖ ÙÖØ Ö Ô Ö Ó Ó ÑÔÐ Ø ÓÒ Ò ¾¼½¼¹¾¼½½ Ó Ø Û Ø Ø Ø Ö ÓÖ Ø ÍË ØÖ Ò Ñ ÓÒ ÓÑ Ø Ð Þ Ò ÓÖ ÖÓÑ Ñ ¹¾¼½½ ØÓ Ñ ¹¾¼½¾º Ì Ô ÖØ ÙÐ Ö Ü ÑÔÐ Ð ÖÐÝ ÑÓÒ ØÖ Ø ÓÛ ÑÙ Ò Ù Ò Ø ÍË ÒØÖ Ð ÛÓÖÐ Ñ Ö Ø ÓÒ Ø Ö Ø Ó Ø ÛÓÖÐ Ò ÓÛ Ð ÖÐÝ Ø ØÖ Ò Ñ ÓÒ ÒÒ Ð Ò Ò Ò Û Ø Ö Ø Ý ÑÔÐ Ý ÓÖ ÑÔ Ò Ø ØÖ Ò Ñ ÓÒ Ó Ó º Ð ÖÐÝ Ø ÒÓØ Ù ÒØ ØÓ ÒÓÛ Û Ñ Ö Ø Ö ÓÒ Ú Ö ÑÔÐ Ý Ò ÓÖ ÑÔ Ò Ò ÔÖ Ö ØÓ Ö Ô ÒØ ÓÒ Ò Ð Ó ØÓ Ô ØÖ Ó Ø Ø ÓÚ Ö Ø Ñ º º Ú ÐÓÔ Ú Ñ Ö Ò Ñ Ö Ø Ï Ñ ÒØ Ø Ö ÙÐØ ÓÒ Ô ÐÐÓÚ Ö Ý Ø Ó Ñ Ö Ø Ú ÐÓÔÑ ÒØ Ù Ò Ø ÁÅ Ð Ø ÓÒ Ó Ú ÐÓÔ Ñ Ö Ò Ò ÖÓÒØ Ö Ñ Ö Ø Ì Ð ½º Ì ÓÒØÖ ÙØ ÓÒ Ó Ó ÓÙÖ ÖÓÑ Ñ Ö Ø Ø Ö ÒØ Ø Ó Ú ÐÓÔÑ ÒØ ØÓ Ø Ö Ô ÒØ Ñ Ö Ø Ö ÐÐÙ ØÖ Ø Ò ÙÖ º ¾½
22 ÙÖ À Ë Ò ÓÖ Ú ÐÓÔ Ò Ñ Ö Ò Ñ Ö Ø Û Ø ± ÓÒ Ò ÒØ ÖÚ Ð Ø ¹ Ñ Ø ÖÓÑ ÕÙ Ø ÓÒ ½ µº Ì ØÖ Ò Ñ ÓÒ ØÓ Ú ÐÓÔ Ñ Ö Ø ÖÓÑ Ñ Ö Ò Ò ÖÓÒØ Ö Ñ Ö Ø Ø ØÓÔ Ô Ò Ð Ó ÙÖ µ Ö Ö Ð Ø Ú ÐÝ Ñ Ðк Ñ Ö Ò Ñ Ö Ø Û Ö Ò Ø ÓÙÖ Ó ÑÔ Ò Ò ÓÖ Ú ÐÓÔ Ñ Ö Ø ÔÖ ÓÖ ØÓ Ø Ò Ú Ö Ñ Ò ÓÙÖ Ó ÒÖ ÔÖ Ñ Ò ÐØ ÓÙ Ø Ô ÙÖ Ò Ð Ø ¾¼¼ º Ì Ø ÖÓÑ ÖÓÒØ Ö Ñ Ö Ø ÓÒ Ú ÐÓÔ Ñ Ö Ø Ö ÑÓÖ ÓÒ Ø ÒØÐÝ ÔÓ Ø Ú ÐØ ÓÙ Ð ÚÓÐ Ø Ð º Ñ Ö Ò Ñ Ö Ø Ú Ö Ú Ð ØØÐ ÒÖ Ò Ë ÔÖ Ñ Ö ÙÐØ Ó Ó ÖÓÑ Ú ÐÓÔ Ñ Ö Ø ½¾ Ò ÓÒØÖ Ø ØÓ Ø ÒØÖ Ò ½¾ Ì Ò Ò ÓÒ Ø ÒØ Û Ø Ò Ø Ðº ¾¼½ µ Û Ó ÓÙÒ Ø Ø Ñ Ö Ò Ñ Ö Ø Ñ ÓÒÓÑ ÐÐÝ ¾¾
23 Ô Ö Ô ÖÝ Ö ÙÑ ÒØ Ó Ã Ñ Ò Ý Ò Ê Ò ÖØ ¾¼¼ µ Û Ð Ó Ò ÖÓÒØ Ö Ñ Ö Ø Ö Ù Ë ÔÖ Ñ Ò Ñ Ö Ò Ñ Ö Ø ÔÖ ÓÖ ØÓ ¾¼¼ ÓÖ Ô Ö Ó ÙÒØ Ð ¾¼½¾º ÁÒ Ø ÓØ Ö Ö Ø ÓÒ ÓÛ Ú Ö ÖÓÒØ Ö Ñ Ö Ø Ö Ú Ù Ø ÒØ Ð ÔÖ Ñ ÙÑ ÑÔÐ Ø ÓÒ ÖÓÑ Ú ÐÓÔ Ñ Ö Ø Ø Ö ¾¼¼ Ò Ô ÖØ ÙÐ ÖÐÝ ÔÓ Ø Ø ¾¼½¾ ÔÖÓ Ð Ñ Ò ÙÖÓÔ Ò ÓÚ Ö Ò Ø Ñ Ö Ø º ÖÓÒØ Ö Ñ Ö Ø Ö Ú ÑÓÖ ÚÓÐ Ø Ð Ø ÖÓÑ Ñ Ö Ò Ñ Ö Ø ¹ ÔÖ ÓÖ ØÓ ¾¼¼ Ñ Ö Ò Ñ Ö Ø Ó Û Ö ÑÔ Ò Ò ÖÓÒØ Ö Ñ Ö Ø ÔÖ ÔÓ ÐÝ ØØÖ Ø Ò ÒÚ ØÓÖ ØÓ Ø Ñ Ö Ø ¹ ÙØ Ø Ö Û Ö Ö Ô ÐÝ Ö Ò Ð Ø ¾¼¼ ÖÐÝ ¾¼¼ Ò ÖÓÒØ Ö Ñ Ö Ø Ù Ö Ö Ñ Ø ÑÔÐ Ø ÓÒ Ó Ó ÙÒØ Ð ÖÐÝ ¾¼½¼º ÙÖ ËÝ Ø Ñ ÐÐÝ ÑÔÓÖØ ÒØ Ò Ú ÓØ Ö Ò Ò Ø Ö Ø Ó Ø ÛÓÖÐ º Ø Ð Ð Ø ÓÒ ÔÖ ÒØ Ò Ì Ð ¾º ÑÓÖ Ö Ð ÒØ Ø Ö Ø º ¾
24 º ÐÓ Ð Ý Ø Ñ ÐÐÝ ÑÔÓÖØ ÒØ Ò ÙÖ ÔÖÓÚ Ô ÐÐÓÚ Ö Ò ØÛ Ò Ò Û Ú Ò Ò Ø ÐÓ ÐÐÝ Ý Ø Ñ¹ ÐÐÝ ÑÔÓÖØ ÒØ ËÁ µ ÓØ Ö Ò Ò ÓØ Ö ØÝÔ Ó Ò Ò Ð Ò Ø ØÙØ ÓÒ º ÁØ ÑÑ Ø ÐÝ Ð Ö Ø Ø Ø Ð Ö Ø Ø Ö ÔÔ Ö ÒØ Ò Ó ÔÖ Ò ÖÓÑ ËÁ Ë ØÓ Ò Ò ÓØ Ö ØÝÔ Ó Ò Ø ØÙØ ÓÒ º Ì ËÁ Ö Ð ÖÐÝ Ò ÑÔÓÖØ ÓÙÖ Ó Ó ÑÔÐ Ø ÓÒ ÓÒ Ø ÒØ Û Ø Ø Ð Ø Ö ØÙÖ Û ÙÔÔÓÖØ Ö ÙÐ Ø Ò Ò ÓÖ Ý Ø Ñ Ö Ö ÓÒ º ÀÓÛ Ú Ö Ø Ò Ù Ò Ó Ó ÑÔÐ Ø ÓÒ ÖÓÑ ËÁ Ë ØÓ ÓØ Ö ÒØ Ø ÒÓØ ÑÓÖ Ò ÒØ Ø Ò ÑÔÐ ¹ Ø ÓÒ ÖÓÑ ÓØ Ö Ò ØÓ ÓØ Ö Ô ÖØ Ó Ø Ò ØÛÓÖ º Ì Ø Û Ð ËÁ Ö ÑÔÓÖØ ÒØ Ø ÒÓØ Ð Ö Ø Ø ØÓ ÒÓÒ¹ Ò Ø Ö Ù Ø ÒØ ÓÒ ØÛ Ò ËÁ Ò ÒÓÒ¹ËÁ Ò Ø ØÙØ ÓÒ º Ï Ð ËÁ Û Ö Ò Ö ÐÐÝ ÓÙÖ Ó ÑÔÐ Ý Ò Ó ÖÓÑ ¾¼¼ ÓÒÛ Ö Ø ÒÓÒ¹ Ò ¹ ØÓÖ ØÖ Ò Ñ ÓÒ Û Ö ÑÔ Ò Ò Ø ØÖ Ò Ñ ÓÒ ØÓ Ø Ò º Ì Ñ Ý Ò Ò Ø ÓÒ Ó Ø Ù ÙÐ ÔÔÐ Ø ÓÒ Ó ÔÓÐ Ý Û Ñ ØÓ ÔÖ Ú ÒØ Ö Ø Ö ØÖ Ø ÓÒ ÖÓÑ Ö Ù Ò ÓÒÓÑ Ø Ú ØÝ Ò Ø Ô Ö Ó ÙØ Û Ø ÓÙØ Ð Ö ÓÙÒØ Ö ØÙ Ð Ø ÙÐØ ØÓ ÓÒ¹ ÐÙ Ú º Ì Ð Ö Ø Ñ ÖÓÑ Ø ËÁ Ò ÒÓÒ¹ËÁ Ø ÒØ ÓÒ Ø Ø ËÁ Ú Ð Ö Ö Ò ÑÓÖ ÖØ Ò ÑÔÐ Ý Ò Ø ÓÒ ÓØ Ö Ò Ø Ò ÓØ Ö Ò Ó ÓÒ ËÁ º º ÁÒ Ü ØÖ ÙØ ÓÒ Ò ÑÓÑ ÒØ Ï Ð Ø Ñ Ò Ð Ø Ö Ð Ô ÐÐÓÚ Ö Ò Ò ½ µ ÔÖÓÚ ÙÑÑ ÖÝ Ó Ò ØÛÓÖ Ø Ú ØÝ Ø Ñ Ý Ó ÙÖ Ö Ø Ð Ó Ö Ð Ú ÒØ Ò ÓÖÑ Ø ÓÒ Ô ÖØ ÙÐ ÖÐÝ Ø Ö ØÖ ÙØ ÓÒ ÝÑÑ ØÖ Ò Ò ÒØ ÙÖØÓ º Ì Ò ÓÖÑ Ø ÓÒ Ô ÖØ ÙÐ ÖÐÝ Ú ÐÙ Ð ÙÖ Ò Ø Ö Û Ò Ò Û Ø Ö Ø Ö ÙÔÔ Ö Ø Ð Ô Ò Ò Ú Ö Ë ÔÖ º º Å Ò Ø Ðº ¾¼½ µµº ÑÓÖ ÓÑÔÐ Ø ÙÑÑ ÖÝ Ó Ô ÐÐÓÚ Ö Ø Ú ØÝ ÑÙ Ø Ø ÓÙÒØ ÒÓØ ÓÒÐÝ Ó Ø ÐÓ Ø ÓÒ ÙØ Ð Ó Ó Ø Ô Ó Ø Ô ÐÐÓÚ Ö Ò Øݺ ÓÖ Ú Ò ÑÓÑ ÒØ t ÓÒ Ñ Ý ÔÔÖÓÜ Ñ Ø Ø ÑÔ Ö Ð ØÖ ÙØ ÓÒ Ó Ô ÖÛ Ô ÐÐÓÚ Ö Ø Ú ÖÒ Ð Ò ØÝ Ø Ñ Ø ÓÒ º º Ö ÒÛÓÓ ¹Æ ÑÑÓ Ø Ðº ¾¼½ µµº ÓÒ Ö Ò h 1 Ú ØÓÖ Ó Ö z = (z 1,...,z h ) Û ÓÚ Ö Ø Ö Ò Ó Ô ÖÛ Ô ÐÐÓÚ Ö Ò Ñ ØÖ Ü C t º Ì Ò ØÝ Ó Ô ÖÛ Ô ÐÐÓÚ Ö Ø Ñ Ø ÖÓÑ ĝ t (z k ) = 1 ( 1 ) n b t n(n 1) i,j=1;i j ( zk c t ) ij K, k = 1,...,h, ½ µ b t Û Ö K ÖÒ Ð Ò b t Ò Û Ø Ø Ø Ñ tº ÌÓ Ò ÙÖ Ø Ø ĝ t (z k ) ÒØ Ö Ø ØÓ ÙÒ ØÝ ÓÚ Ö Ø Ð Ø Ö Ò Ó Ö ÔÓ ÒØ Ø ÓÐÐÓÛ Ò Ø Ò Ö ÒÓÖÑ Ð Þ Ø ÓÒ ÑÔÐÓÝ ˆf t (z k ) = ĝt(z k ) ), ½ µ RIE (ĝ t ) Û Ö RIE (ĝ t ÒÓØ ÒÙÑ Ö Ð Ê Ñ ÒÒ ÙÑ Ó ĝ t = (ĝ t (z 1 ),...,ĝ t (z h )) º ÓÐÐÓÛ Ò Ë ÐÚ Ö¹ Ñ Ò ½ µ Ù Ò ÖÒ Ð Û Ø Ø ÖÙÐ ¹Ó ¹Ø ÙÑ Ò Û Ø b t = 1.06ˆτ t (n(n 1)) 0.2 ÓÒ Ö Ò Ñ Ö Û Ö τ t Ø ÖÓ ¹ Ø ÓÒ Ð Ø Ò Ö Ú Ø ÓÒ Ó c t ij º ÀÓÛ Ú Ö Ú Ò Ø Ø Ø Ô ÐÐÓÚ Ö Ò ØÝ Ü Ø Ô ÖØÙÖ ÖÓÑ ÒÓÖÑ Ð ØÝ Û Ò ÛÓÖ Ò Û Ø Ë Ø ¾
25 Ö Ø Ò Ð Ø Û Ñ Ø ÔÖÓÒÓÙÒ º ½ ÁÒ Ø Ø ÓÒ Û ÓÑ Ò Ø Ò ÓÖÑ Ø ÓÒ ÓÒ Ô ÖÛ ÓÒÒ Ø Ò C t Û Ø Ø Ö Ò Ö¹ Ù Ð ØÝ ÔÔÖÓ ØÓ Ø Ø Ò Ò ØÛÓÖ Ö Ø ÓÒ Ò Ò Ò Ó ÐÐ Ó Ø Ðº ¾¼½¾µ Ò Å ÖØÓÒ Ø Ðº ¾¼½ µº Ì ÔÔÖÓ Ö Ù Ø Ñ Ò ÓÒ Ð ØÝ Ó Ø ÔÖÓ Ð Ñ Ý Ö ÑÓÚ Ò ÐÐ ÒÓÒ¹ Ö Ò Ö Ù Ð Ò º ÐÐ Ó Ø Ðº ¾¼½¾µ ÔÖÓÔÓ Ø Ø Ö Ò Ö¹ Ù Ð ØÝ Ð Ò Ú Ò Ú ÒØ ÓÚ Ö Ö Ø ÓÖÖ Ð Ø ÓÒ Ò ÔÖÓÚ Ò Ð ¹Ð Ñ Ò ÓÒº Ë Ò ÒØ Ö Ò Ö Ù Ð ØÝ ÖÓÑ ÒØ ØÝ i ØÓ ÒØ ØÝ s Ò Ø Ø Ø Y i Ø Ð Ø ÓÒ Ò ÒØ Ð ÔÖ Ø Ò Ø Ú ÐÙ Ó Y s Ò Ø Ò Ø Ø Ø Ô Ö Ú Ö Ó ÒØ ØÝ i ÙÐØ Ò ÔÖ Ø Ø Ô Ö Ú Ö Ó ÙÐØ Ó ÒØ ØÝ sº Ì Ó Ø Ò ØÛÓÖ ÓÒ ØÖÙØ ÖÓÑ Ø Ö Ò Ö Ù Ð ØÝ Ð Ò Ö ÔÖ ÒØ ÔÖ ØÓÖ Ó ÒÓ ³ Ô Ö Ú Ö Ó ÙÐغ ÅÓÖ ÓÚ Ö Ö Ò Ö Ù Ð ØÝ Ø Ð Ñ Ô Ð ÖÐÝ ØÓ Ø Ü Ø Ò ÑÔ Ö Ð Ö Ñ ÛÓÖ ÓÖ Ñ ÙÖ Ò Ò Ø Ø Ò ÓÒØ ÓÒ ÙÖ Ò Ò Ò Ð Ö Ú Ø ÓÖÑ Ø ÓÒ Ò Ö Ò Ó Ð Ò Ø ÓÚ Ö Ö Ò Ö Ñ ÛÓÖ ÓÖ Ø ÔÖÓÚ Ò ÙÒ Ý Ø Ðº ¾¼¼ µµº ÇÒ Î Ê ÓÖÑ Ó Ø ÑÓ Ð Ø Ñ Ø ÖÓÑ µ Ö Ò Ö Ù Ð ØÝ ØÛ Ò Ë ÔÖ Y i Ò Y s Ò Ù Ò Ø Ï Ð Ø Ø WT = [e ˆη] [e( V (Y Y) 1 )e ] 1 [e ˆη], ½ µ Ò Û Y Ø Ñ ØÖ Ü Ó Ò Ô Ò ÒØ Ú Ö Ð Ö ÔÖ ÒØ Ý Ë ÔÖ ˆη ÒÓØ Ø ÖÓÛ Ú ØÓÖ Þ Ó ÒØ Ó Î Ê Ù ÖÐ Ö V = T 1 T t=1 ˆε tˆε t Ò e Ø k 2(2k+1) Ð Ø ÓÒ Ñ ØÖ Ü e = º º º º º º ºº º º º º ÖÓÛ Ó e Ð Ø ÓÒ Ó Ø Ó ÒØ ØÓ Ø ØÓ Þ ÖÓ ÙÒ Ö Ø ÒÓÒ¹ Ù Ð ÝÔÓØ Y i Y s º Ì Ö ÙÐØ Ó Ø Ï Ð Ø Ø Ò Ø Ò Ö Ò Ö Ù Ð ØÝ Ö Ö ÓÖ Ò ÖÝ ÒØÖ Ò Ñ ØÖ Ü Ã Û Ö ã is = à = [ã is ], { 0, Yi Ó ÒÓØ Ö Ò Ö Ù Y s 1, Y i Ö Ò Ö Ù Y s. Å ØÖ Ü Ã Ù ØÓ ÓÒ ØÖÙØ Ø Ö Ø ÓÒ Ð ØÛ Ò ÓÚ Ö Ò Ò Ò º Ú Ò Ø Ø Ñ Ø Ó Ø Ñ ØÖ Ü Ã Ò Ø Ô ÐÐÓÚ Ö Ñ ØÖ Ü C Ø ØÖÙØÙÖ Ó Ø Û Ø Ñ ØÖ Ü Ò Ö Ø Ö Þ Ã = à C, Û Ö Ø À Ñ Ö ÔÖÓ Ùغ Ì Ð Ñ ÒØ Ó Ø ÒÝ Ñ ØÖ Ü Ã ÒÓÛ ÔØÙÖ Ø ÓÒÒ Ø Ò ØÛ Ò ÒØ Ø ÓÒ Ø ÓÒ Ð ÓÒ Ø Ò ÒØ Ù Ð Ð Ò ØÛ Ò Ø Ñº Ì ½ Ò ÓÖ Ò Ð Ô ÐÐÓÚ Ö Ò Ü Ó Ø Ò Ö Ø Û Ò ¹ÑÓ Ð Ò ÓÑ ¹ Ö ÕÙ Ö Ò Ö ÙÐ ÖÓ Ù ØÒ ÒÐÙ Ò ÐØ ÖÒ Ø Ú ÖÒ Ð Ò Ò Û Ø º ¾
26 Ò ØÛÓÖ Ò Ý Ø ÒÝ Ñ ØÖ Ü Ã ÓÛ Ø ÔÖ ØÓÖ Ó Ø Ö Ó ÙÐØ Ù Ø ØÓ Ó ÔØÙÖ Ý Ø Ñ ØÖ Ü Cº Í Ò Ø ÒØÖ Ó Ø Ñ ØÖ Ü Ã Ý Ø Ñ¹Û ÓÑÔÐ Ø Ò Ñ ÙÖ C = n i,j=1ã ij i j n i,j=1 Ì Ò Ü ØÖ ÙØ ÓÒ ÓÒ Ø ÓÒ Ð ÓÒ Ø Ö Ò Ö Ù Ð Ò ØÛ Ò ÒØ Ø Ó Ø Ò Ý ÔÔÐÝ Ò ÕÙ Ø ÓÒ ½ µ Ò ½ µ ØÓ Ø ÒÓÒ¹ ÓÒ Ð ÒØÖ Ó Ø Ñ ØÖ Ü Ã tº i j c ij. ¾¼µ Jan-2005 Jan-2006 Jan-2007 Jan-2008 Jan-2009 Jan-2010 Jan-2011 Jan-2012 Jan-2013 Mean 1 Variance Jan-2005 Jan-2006 Jan-2007 Jan-2008 Jan-2009 Jan-2010 Jan-2011 Jan-2012 Jan Skewness Sept 15 Jan-2005 Jan-2006 Jan-2007 Jan-2008 Jan-2009 Jan-2010 Jan-2011 Jan-2012 Jan Kurtosis Jan-2005 Jan-2006 Jan-2007 Jan-2008 Jan-2009 Jan-2010 Jan-2011 Jan-2012 Jan-2013 ÙÖ ½¼ ÅÓÑ ÒØ Ó Ø Ô ÐÐÓÚ Ö Ò ØÝ Ó Ø Ò ÖÓÑ ÕÙ Ø ÓÒ ½ µ Ò ½ µº Ð Ð Ò ¹ ÐÐ ½¼ Ö ¹ Ò Ò Ð Ò Ø ØÙØ ÓÒ Ö Ò ¹ ÓÚ Ö Ò º ¾
27 Ì Ö Ø ÓÙÖ ÑÓÑ ÒØ Ó Ø À Ô ÐÐÓÚ Ö Ò Ü Ø Ñ Ø ÓÒ Ø ÓÒ Ð ÓÒ Ø Ö Ò Ö Ù Ð Ò ÓÖ ÐÐ ½¼ ÒÓ Ö ÓÛÒ Ò ÙÖ ½¼ Û Ø Ø ÑÓÑ ÒØ ÓÖ Ø Ò Ò Ð ÓÑÔ Ò Ò ÓÚ Ö Ò Ò Ú Ò Ô Ö Ø ÐÝ Ø Ö Ò Ö Ò Ð Ò Ö Ô Ø Ú Ðݺ Ì Ö Ø Ò Ö ÑÑ Ø ÐÝ ÔÔ Ö Òغ Ö Ø ÓØ ÛÒ Ò ÙÖØÓ Ó Ø ÓÑ Ò Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ Ò ØÛÓÖ Ö ÔÓ Ø Ú Ò Ó¹ÑÓÚ ÙÖ Ò Ø Û ÑÔÐ Ò ÒØ ÙÐØ Ö ÔÖ Ñ Ò Ø Ò Ò Ð Ò Ù ØÖݺ Ò ÒØ Ö Ø Ò Ô ØØ ÖÒ Ò Ø ÛÒ Ó Ø Ò ØÛÓÖ Ó ÖÚ ÓÒ Ø Ö Ø Ý Ó Ø ½ Ø Ó Ë ÔØ Ñ Ö ¾¼¼ µ Û Ò Ø Ø Ö ÑÓÑ ÒØ ÙÑÔ ÙÔ Ý ÑÓÖ Ø Ò ÔÓ ÒØ º Ì Ò Ò ÓÒ Ø ÒØ Û Ø ÖÝ Ø Ðº ¾¼½¼µ Û Ó Ö Ù Ø Ø Ö ÑÓÑ ÒØ Ö Ò ÓÖÑ Ø Ú Ò ÔÖ Ø Ò ÓÒØ ÓÒº Ë ÓÒ Ø Ô ÐÐÓÚ Ö Ú Ö Ò ÓÖ ÐÐ Ø Ö Ò ØÛÓÖ ÒÖ ÖÓ Ø ÑÔÐ º ÅÓÖ ÓÚ Ö Ø Ö Ø ÒØÐÝ Ó ÖÚ Ð Ø ÖÓÑ ÔÖ ¹¾¼¼ ØÓ ÔÓ Ø¹¾¼¼ Ò Ø Ð Ú Ð Ò ÚÓÐ Ø Ð ØÝ Ó Ó Ø Ò º Ì Ö Û Ð ÓÖ Ò ÙÖ Ò Ø ÚÓÐ Ø Ð ØÝ Ó Ø ÓÑ Ò Ò ØÛÓÖ Ñ ÒÐÝ Ö Ú Ò Ý Ò Ò Ð Ò Ø ØÙØ ÓÒ ¹ Ø Ö Ø ÙÖÓÔ Ò Ø Ö Ó ¾¼½¼ Ø Ú Ö Ò Ó Ø ÓÑ Ò Ò ØÛÓÖ Ñ Ò Ø ÖÓÑ ÓØ Ò Ò Ð Ò Ø ØÙØ ÓÒ Ò ÓÚ Ö Ò º ÇÚ Ö ÐÐ Ø ÓÚ Ö Ò Ò Ø Ò Ù ÖÓÑ Ø Ò Ò Ð Ò Ø ØÙØ ÓÒ Ò Ø Ø Ø ÒÖ Ò Ú Ö Ò ÛÒ Ò ÙÖØÓ ÓÑ Ð Ø Ö Ò Ø ÑÔÐ ÐÓ Ö ØÓ Ø ÔÖÓ Ð Ñ Ó Ø Û Ø Ø Ö Ò Ù ÕÙ ÒØ ÙÖÓÔ Ò ÓÚ Ö Ò Ø Ö º ÌÓ ÙÑÑ Ö Þ Ø ÚÓÐÙØ ÓÒ Ó Ø Û ÓÐ Ö ØÖ ÙØ ÓÒ ÓÖ Ø Ñ t Û ÓÒ ØÖÙØ ÕÙ Ò Ó t = 1,...,T Ô ÐÐÓÚ Ö Ò Ø º Ì ÔÖ ¹Ö Ô Ö Ó ÓÒ Ö Ò Ñ Ö Ö Ø Ö Þ Ý Ò ØÝ f nc Û ÓÑÔ Ö Û Ø f cr Ò ØÝ ÙÖ Ò Ö º Í Ò Ø ÓÐÐÓÛ Ò ÓÑÑÓÒ Ú Ö Ò Ö Ø Ö Ò ÚÓÐÙØ ÓÒ Ó Ø Ô ÐÐÓÚ Ö Ò ØÝ ÖÓÑ ÒÓÒ¹Ö ØÓ Ö Ô Ò DH(ˆf cr,f nc ) = sup z ˆf cr f nc /sup z f nc (z), ˆ DM(ˆf cr,f nc ) = ˆf cr (z)dz f nc (z) dz, ¾½µ ¾¾µ Û Ö ˆf cr Ø Ø Ñ Ø Ò ØÝ ÙÖ Ò Ø Ö DH Ø À Ð ÖØ ÒÓÖÑ Ò DM Ø ØÖ ÙØ ÓÒ Ñ Ö Ò º Ó Ø ÕÙ ÒØ Ø ÒÓÒ¹Ò Ø Ú Ò Ø Ø Ú ÐÙ Þ ÖÓ ˆf cr = f nc º ÅÓÖ ÓÚ Ö DM [0,2] Û Ø DM = 2 Û Ò ˆf cr Ò f nc Ó ÒÓØ ÓÚ ÖÐ Ô Ø ÐÐ ÓÚ Ö Ø Ð Ø Ö Ò Ó Ö ÔÓ ÒØ º Í Ò Ø Ñ Ô ÐÐÓÚ Ö Ò Ø ÓÖ Ø ÓÑ Ò Ò ØÛÓÖ Ò ÙÖ ½¼ Û Ø Ñ Ø DH Ò DM ÕÙ ÒØ Ø ÓÖ Ý tº ÒÓÒ¹Ö Ò ØÝ f nc Ó Ø Ò ÖÓÑ Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ô ÐÐÓÚ Ö Ò Ñ Ö ¾¼¼ º ÓÐÐÓÛ ÖÓÑ ÙÖ ½½ ÓØ DH Ò DM Ñ ÙÖ ÓÛ Ñ Ð Ö Ô ØØ ÖÒ Ò Ñ ÐÝ ØÛ Ò ¾¼¼ Ò ¾¼¼ Ø Ö Ò ØÛ Ò Ø Ö Ò ÒÓÒ¹Ö Ô ÐÐÓÚ Ö ØÖ ÙØ ÓÒ ÒÖ Ò Ú Ø Ô Ò ÂÙÐÝ ¾¼½½º Ì Ô ÓÒÙÖ Û Ø Ø ÒÒ Ò Ó Ø ÓÒ ÓÒÓÑ Ù ØÑ ÒØ ÔÖÓ Ö ÑÑ Û Ò ÙÖÓ Ö Ð Ö Ö ØÓ ÜØ Ò Ö Û ÐÐ ÁÖ Ò ÈÓÖØÙ Ù µ ÐÓ Ò Ö Ô ÝÑ ÒØ Ô Ö Ó ÖÓÑ Ý Ö ØÓ Ñ Ò ÑÙÑ Ó ½ Ý Ö Ò ØÓ ÙØ ÒØ Ö Ø Ö Ø ØÓ º ±º Ø Ö ÂÙÐÝ ¾¼½½ Ø Ú Ö Ò Ø Ý Ø Ø Ñ Ð Ú Ð Ò Ó Ô Ö Ò Ø Ò Ò Ð Ò ÓÚ Ö Ò Ë Ñ Ö Ø ÓÒ ÖÑ Ò Ø Ö ÙÐØ Ó Ç Ò È ØØÓÒ ¾¼½ µ Ø Ø Ø Ó ÒØ ÔÖÓ Ð ØÝ Ó ØÖ Ñ ÙÖ Ó Ý Ø Ñ Ö µ Ù Ø ÒØ ÐÐÝ Ö Ø Ö ¾¼½½ Ø Ò Ò Ø ÔÖ ¹Ö Ô Ö Ó º Ì Ò Ò ¾
28 Ð Ó ÓÒ Ø ÒØ Û Ø Ø Ô ØØ ÖÒ Ó ÒÖ Ò Ú Ö Ò ÖÓÑ ÙÖ ½¼ Û ÐÐÓÛ ØÓ ÓÒ Ö ÚÓÐ Ø Ð ØÝ Ò Ø Ë Ñ Ö Ø Ø Ñ Ò ÓÙÖ Ó Ý Ø Ñ Ö º ÇÚ Ö ÐÐ Ø Ò ÐÝ Ó Ø Ô ÐÐÓÚ Ö Ò ØÝ ÖÓ Ö Ò Ó ÑÓÑ ÒØ Ô ÖÑ Ø Ô Ö ÙÒ Ö Ø Ò Ò Ó Ø Ò Ò ÒØ ÖÓÒÒ Ø Ò Ó Ø ÐÓ Ð Ë Ñ Ö Øº 0.7 Hilbert norm Jan-2005 Jan-2006 Jan-2007 Jan-2008 Jan-2009 Jan-2010 Jan-2011 Jan-2012 Jan Distribution mass difference Jan-2005 Jan-2006 Jan-2007 Jan-2008 Jan-2009 Jan-2010 Jan-2011 Jan-2012 Jan-2013 ÙÖ ½½ À Ð ÖØ ÒÓÖÑ Ò ØÖ ÙØ ÓÒ Ñ Ö Ò Ø Ñ Ø ÖÓÑ ÕÙ Ø ÓÒ ¾½µ Ò ¾¾µ Ö Ô Ø Ú ÐÝ ÓÖ ÐÐ ÒØ Ø º ÓÒÐÙ ÓÒ Ì Ô Ô Ö ÓÛÒ ÓÛ Ò ÐØ ÖÒ Ø Ú ÓÑÔÓ Ø ÓÒ Ó Ø Ò ÓÖÑ Ø ÓÒ Ú Ð Ð Ò Î Ê Ö ÔÖ ÒØ Ø ÓÒ Ó Ø ØÖ Ò Ø Ó Ò ØÛÓÖ Ð Ò ØÛ Ò Ñ Ö Ø Ò ÔÖÓÚ Ò ÓÖÑ Ø ÓÒ ÓÒ ÓÙÖ Ö Ø ÓÒ Ò Û Ø Ö Ð Ò ÑÔÐ Ý ÓÖ ÑÔ Ò Ø ØÖ Ò Ñ ÓÒ Ó Ó ÖÓ Ò ØÛÓÖ º Ï ÓÛ ÓÛ Ø ÛÓÖ Ö Ð Ø ØÓ Ø ÔÓÔÙÐ Ö ÙÒ Ò µ ÓÐ Ò ÐÑ Þ Ô ÐÐÓÚ Ö Ò Ü Ò Ø ÜØÖ Ò ÓÖÑ Ø ÓÒ Û Ò Ó Ø Ò Ý ÒÓÛ Ò ÒÓØ ÓÒÐÝ Ø ÓÙÖ Ö Ø ÓÒ Ò Ö Ð Ø Ú Þ Ó Ó ÙØ Ð Ó Ø Ò ÑÔÐ Ý Ò ÓÖ ÑÔ Ò Ò µ Ó Ø Ö ÑÔ Øº Ï ÑÔ Ø Ø Ø Ö ÒØ Ò Ò ÖÓÑ Ö Ø ÓÒº Ì Ö Ø ÓÒ Ó Ó Ò Ø Ø ÓÛ Ó Ù Ð Ú ÒØ Ò ÓÒ ÒÓ ØÓ Ø ÓØ Ö ÒÓ º Ì ÓÒØÖ ÙØ ÓÒ Ó Ò Ò Ò Ø Û Ø Ö Ø Ø ØÖ Ò Ñ ÓÒ ÔÓ Ø Ú ÓÖ Ò Ø Ú ÑÔ Ø ÓÒ Ø ÚÓÐ Ø Ð ØÝ Ó Ø Ø Ö Ø ÒÓ º Ì ÑÔÓÖØ ÒØ ÓÖ ÔÓÐ ÝÑ Ö ÒÓØ ÐÐ ØÖ Ò Ñ ÓÒ Ò Ö ÐÝ ÒÖ ÚÓÐ Ø Ð ØÝ Ò Ø Ñ Ý Ú ÒØ ÓÙ ÙÖ Ò Ô Ö Ó Ó ØÖ ØÓ Ð ØÓ ÒØ Ý Ò Ø Ö Ø ÒÒ Ð Û ¾
29 Ü Ö Ø ÓÒ Ø ÓÒ Û Ð Ø ÐÐÓÛ Ò Ø Ó Û ÐÑ Ø Ñ ØÓ Ö Ñ Òº Ò Ü ÑÔÐ Ó Û Ö Ø Ñ Ò Ñ Ö Ø Ò Ø Ð Ø Ö ØÙÖ ÓÒ ÖÒ Ø ÖÓÐ Ó ÓÖع Ð Ö ØÖ Ø ÓÒ º Ì ÔÖÓÔÓ ÒØ ÖÓÒÒ Ø Ò Ñ ÙÖ ÓÒ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ý ØÓ ÑÔÐ ¹ Ñ ÒØ Ò Ø Ó ÒÓØ Ö ÕÙ Ö ÖÓÐÐ Ò Û Ò ÓÛ Ø Ñ Ø ÓÒ ÓÖ ÒÝ ÒÓÖÑ Ð Þ Ø ÓÒ Ñ ÐØ ÓÙ Ø Ò ÑÔÓ Ö µº Ì ØÖ ÙØ ÓÒ Ó ÓÙÖ Ò Ü ÝÑÔØÓØ ÐÐÝ ÒÓÖÑ Ðº Ì ÓÖØ Ó ÓÒ Ð ØÝ Ó Ð Ñ ÒØ Ó ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ô ÖÑ Ø Ù ØÓ Ó Ø Ò Ò ÐÝØ Ð Ø Ò Ö ÖÖÓÖ Ó Ø ÔÖÓÔÓ Ò Üº ÇÙÖ ÑÔ Ö Ð Ò Ò ÓÒ ÖÑ Ø Ø ÓØ ÓÚ Ö Ò Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ Ò ÒØÐÝ ÓÒ¹ ØÖ ÙØ ØÓ Ý Ø Ñ Ö Ó Ø ÐÓ Ð Ë Ñ Ö Øº ÙÖ Ò Ø ÓØ ÓÚ Ö Ò Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ Ò Ù ÓÒÒ Ø Ò Ó Ø Û Ø ÔÓ Ø Ú Ú Ö Ø ÓÒ Ò Ë ÔÖ Û Ð Ø Ö Ø ÙÖÓÔ Ò Ø Ö ÔÖ Û Ö Ð Ó ÔÖ ÒØ ÓÖ ÓÚ Ö Ò Ù Ö º Ò Ö ÓÙÒ ØÓ Ø Ð Ö Ø ÔÖ Ö Ó Ó Û Ð Ò Ò Ð Ò Ø ØÙØ ÓÒ Ñ ÒÐÝ Ö Ú Ý Ø Ñ Ö ÖÓÑ ÓØ Ö º Ú ÐÓÔ Ò Ñ Ö Ò ÓÙÒØÖ ÔÖ Ò ÒØ ÑÓÙÒØ Ó Ö Û Û ÓÖ Ý ÖÓÒØ Ö Ñ Ö Ø º ËÝ Ø Ñ ÐÐÝ ÑÔÓÖØ ÒØ ÐÓ Ð Ò Ù ÓÒÒ Ø ÓÒ Û Ø ÓØ Ö Ò Ö Ø Ð Ð Ò Ò Ø ÓÑ Ò Ò ØÛÓÖ º ¾
30 Ê Ö Ò ÑÓ ÐÙ ÖÚ Ð Ó ÎºÅº Ò Ì Þ¹Ë Ð º ¾¼½¾º Ì Ò ØÛÓÖ ÓÖ Ò Ó Ö Ø ÙØÙ Ø ÓÒ º ÓÒÓÑ ØÖ ¼ ½ ¾¼½ º ÑÓ ÐÙ ÇÞ Ð Ö Ò Ì Þ¹Ë Ð º ¾¼½ º ËÝ Ø Ñ Ö Ò Ø Ð ØÝ Ò Ò Ò Ð Ò ØÛÓÖ º Ñ Ö Ò ÓÒÓÑ Ê Ú Û ½¼ ¼ º ÐØ Ö º Ò Ý Ö º ¾¼½ º Ì ÝÒ Ñ Ó Ô ÐÐÓÚ Ö Ø ÙÖ Ò Ø ÙÖÓÔ Ò ÓÚ Ö Ò Ø ØÙÖÑÓ Ðº ÂÓÙÖÒ Ð Ó Ò Ò Ò Ò Ò ¾ ½ ½ º ºÀº Ò Ê Ö ÓÒ ÅºÈº ¾¼½ º ÅÓ ÖÒ Þ Ò ÁÒ ÙÖ Ò Ê ÙÐ Ø ÓÒº ÂÓ Ò Ï Ð Ý ² ËÓÒ º ÐÐ Ó Åº ØÑ Ò Ý Åº ÄÓ º Ò È Ð ÞÞÓÒ Äº ¾¼½¾º ÓÒÓÑ ØÖ Ñ ÙÖ ÓÖ ÓÒÒ Ø ¹ Ò Ò Ý Ø Ñ Ö Ò Ø Ò Ò Ò Ò ÙÖ Ò ØÓÖ º ÂÓÙÖÒ Ð Ó Ò Ò Ð ÓÒÓÑ ½¼ º ÓÖ Ó º Ò º ¾¼½ º ÍÒÓÒÚ ÒØ ÓÒ Ð ÑÓÒ Ø ÖÝ ÔÓÐ Ö ¹ ÔÔÖ Ðº ÁË ÏÓÖ Ò È Ô Ö ÆÓ ¼º Á˺ Ó Ø Ò º Ò ÐÑ Þ Ãº ¾¼½ º ÀÓÛ ÓÒÒ Ø Ø ÐÓ Ð ËÓÚ Ö Ò Ö Ø Ê Æ ØÛÓÖ ËËÊÆ ÛÓÖ Ò Ô Ô Öº Ò Éº Ð Ö Ó º À º Ò Ù º ¾¼½ º Ò Ò Ð Ö ÍË ÙÒÓÒÚ ÒØ ÓÒ Ð ÑÓÒ Ø ÖÝ ÔÓÐ Ý Ò ÒØ ÖÒ Ø ÓÒ Ð Ô ÐÐÓÚ Ö º ÂÓÙÖÒ Ð Ó ÁÒØ ÖÒ Ø ÓÒ Ð ÅÓÒ Ý Ò Ò Ò ¾ ½º Ñ Ö Ö Åº ÓÐ º º Ä Ù Äº Ò ÐÑ Þ Ãº ¾¼½ º Ø Ñ Ø Ò ÐÓ Ð Ò Ò ØÛÓÖ ÓÒÒ Ø Ò º ÈÁ Ê ÏÓÖ Ò È Ô Ö ½ ¹¼¾ º È ÒÒº ÁÒ Ø ØÙØ ÓÖ ÓÒÓÑ Ê Ö º ÑÓÒ Èº º ½ ¾º Ö Ø Ñ Ò Ñ Ò Ñ ÒØ Ò Ö ÕÙ Ð Ö ÙѺ ÂÓÙÖÒ Ð Ó ÈÓÐ Ø Ð ÓÒÓÑÝ ¼ ½ º ÓÐ º º Ò ÐÑ Þ Ãº ¾¼¼ º Å ÙÖ Ò Ò Ò Ð Ø Ö ØÙÖÒ Ò ÚÓÐ Ø Ð ØÝ Ô ÐÐÓÚ Ö Û Ø ÔÔÐ Ø ÓÒ ØÓ ÐÓ Ð ÕÙ ØÝ Ñ Ö Ø º ÓÒÓÑ ÂÓÙÖÒ Ð ½½ ½ ½ ½º ÓÐ º º Ò ÐÑ Þ Ãº ¾¼½ º ÇÒ Ø Ò ØÛÓÖ ØÓÔÓÐÓ Ý Ó Ú Ö Ò ÓÑÔÓ Ø ÓÒ Ñ ÙÖ Ò Ø ÓÒÒ Ø Ò Ó Ò Ò Ð ÖÑ º ÂÓÙÖÒ Ð Ó ÓÒÓÑ ØÖ ½ ¾ ½½ ½ º ÓÐ º º Ò ÐÑ Þ Ãº ¾¼½ º Ò Ò Ð Ò Å ÖÓ ÓÒÓÑ ÓÒÒ Ø Ò º ÄÓÒ ÓÒ ÇÜ ÓÖ ÍÒ Ú Ö ØÝ ÈÖ º ÓÐ º º Ò ÐÑ Þ Ãº ¾¼½ º ÌÖ Ò ¹ ØÐ ÒØ ÕÙ ØÝ ÚÓÐ Ø Ð ØÝ ÓÒÒ Ø Ò ÍË Ò ÙÖÓÔ Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ ¾¼¼ ¹¾¼½ º ÂÓÙÖÒ Ð Ó Ò Ò Ð ÓÒÓÑ ØÖ ½ ½ ½¾ º ٠ź Ò È ÐØÓÒ Ò Ìº º ¾¼½ º Ò Ý Ø Ñ Ö Ò ÔÖ Ø Ò Ý Ø Ñ Ú ÒØ º ÂÓÙÖÒ Ð Ó Ò Ò Ò Ò Ò ¾½ ¾½ º ÙÒ Ý Åº Ò È Ò ºÊº ¾¼¼¼º ØÖÙØÙÖ Ð Î Ê Ó Ø Ù ØÖ Ð Ò ÓÒÓÑݺ ÓÒÓÑ Ê ÓÖ ¾½ ¾º ¼
31 ÙÒ Ý Åº ÖÝ Êº ÓÒÞ Ð Þ¹À ÖÑÓ ÐÐÓ º Ò Å ÖØ Ò ÎºÄº ¾¼¼ º ÑÔ Ö Ð ÑÓ ÐÐ Ò Ó ÓÒØ Ó Ò Ö Ú Û Ó Ñ Ø Ó ÓÐÓ º ÉÙ ÒØ Ø Ø Ú Ò Ò ¾ º ÙÒ Ý Åº Å ÐÙÒÓÚ º Ì ÓÖÔ Ëº Ò Ò Åº ¾¼½ º Ò Ó ÒÓÙ Ö Ø Ò Ò ÓÒØ ÓÒ Ù Ò ÑÓÓØ ØÖ Ò Ø ÓÒ ØÖÙØÙÖ Ð Ê Àº ÂÓÙÖÒ Ð Ó Ò Ò ² Ò Ò ½ º ÙÒ Ý Åº À ÖÚ Ý Âº Ò ÎÓÐ ÓÚ Îº ¾¼½ º Ì Ò Ò ÒØ ÖÒ Ø ÓÒ Ð Ò ØÛÓÖ Ó ÓÚ Ö Ò Ø Ò Ò Ò Ð Ò Ø ØÙØ ÓÒ º Ù ÓÒ Ô Ô Ö ÍÒ Ú Ö ØÝ Ó Ì Ñ Ò ¾¼½ ¼½º ÙÒ Ý Åº ÄÙ Ò Åº Ò Î Ö º ¾¼½ º ËÝ Ø Ñ Ö Ò Ø ÍË ÁÒØ ÖÓÒÒ Ø Ò ÖÙ Ø Ö Öº ÍÒÔÙ Ð Ñ ÒÙ Ö Ôغ ÖÝ Êº Å ÖØ Ò ÎºÄº Ò Ì Ò º ¾¼½¼º Ò Û Ð Ó Ø Ø Ó ÓÒØ ÓÒ Û Ø ÔÔÐ Ø ÓÒ º ÂÓÙÖÒ Ð Ó Ù Ò Ò ÓÒÓÑ ËØ Ø Ø ¾ ¾ º Ñ ÓÖØ Äº Ò Âº Ò Ì Ø ÖÓÒ Ãº ¾¼½ º Ò Ò Ð ØÖÙØÙÖ Ò ÖÓÛØ º ËËÊÆ ÏÓÖ Ò È Ô Ö ÆÓ ¾ ½¼ º ËËÊƺ Ö Ø Äº Ã Ô Ø Ò Ó º Ï Ø Ö ÐØ º Ò º ¾¼½ º Ø Ñ Ø Ò Ø ÝÒ Ñ Ò Ô Ö Ø Ò Ó Ò Ò Ð Ò ØÛÓÖ Û Ø Ò ÔÔÐ Ø ÓÒ ØÓ Ø Ø ÖÐ Ò ÑÓÒ Ý Ñ Ö Øº Ì ÂÓÙÖÒ Ð Ó ÔÔÐ ÓÒÓÑ ØÖ ½ º Ð ÖÑ Ò Èº Ò ÓÙÒ ÀºÈº ¾¼½ º ÀÓÛ Ð ÐÝ ÓÒØ ÓÒ Ò Ò Ò Ð Ò ØÛÓÖ ÂÓÙÖÒ Ð Ó Ò Ò Ò Ò Ò ¼ º Ö ÒÛÓÓ ¹Æ ÑÑÓ Åº Æ ÙÝ Ò Îº Ò Ë Ò º ¾¼½ º Ï Ø³ Ñ Ò ÝÓÙÖ ÓÚ Ö Ò Ö ØÖ Ò Ñ ÓÒ ÙÖ Ò Ø ÙÖÓÔ Ò Ø Ö º ÍÒÔÙ Ð Ñ ÒÙ Ö Ôغ À Ð Ò º º ¾¼¼ º Ê Ø Ò Ò Ø Ò Ò Ð Æ ØÛÓÖ º ËÔ º Ò Ó Ò Ð Ò º À٠Рº Ò ÊÓ Ò ÓÒ ÈºÅº ¾¼½¼º Ë ÑÔ Ô Ö Ñ ØÖ Ò Ö Ò Ò ÑÙÐØ Ú Ö Ø Ö Ø ÓÒ ÐÐÝ Ó ÒØ Ö Ø Ý Ø Ñ º ÂÓÙÖÒ Ð Ó ÓÒÓÑ ØÖ ½ ¾ ½½º ÂÓÖ ÓÒ Èº Ò Ò º ¾¼¼ º ÓÓ Ò Ö Ø ÓÒØ ÓÒ Ú Ò ÖÓÑ Ö Ø ÙÐØ Û Ô º ÂÓÙÖÒ Ð Ó Ò Ò Ð ÓÒÓÑ ¼ º Ã Ð Ò Ø ÓÛ Åº ¾¼½¾º ÙÖÓÞÓÒ ÓÚ Ö Ò ÓÒØ ÓÒ Ú Ò ÖÓÑ Ø Ë Ñ Ö Øº ÂÓÙÖÒ Ð Ó ÓÒÓÑ Ú ÓÖ Ò ÇÖ Ò Þ Ø ÓÒ º Ã Ñ Ò Ý º Ò Ê Ò ÖØ º ¾¼¼ º Ì ÒØ Ö Ò Ø È Ö Ô ÖÝ Ì ÐÓ Ð Þ Ø ÓÒ Ó Ò Ò Ð ÌÙÖÑÓ Ðº ÏÓÖ Ò È Ô Ö º Æ Êº ÃÓÓÔ º È Ö Ò ÅºÀº Ò ÈÓØØ Ö ËºÅº ½ º ÁÑÔÙÐ Ö ÔÓÒ Ò ÐÝ Ò ÒÓÒÐ Ò Ö ÑÙÐØ ¹ Ú Ö Ø ÑÓ Ð º ÂÓÙÖÒ Ð Ó ÓÒÓÑ ØÖ ½½ ½ º Ä Ø ÔÓ Ð Àº ½ ¼º ÝÑÔØÓØ ØÖ ÙØ ÓÒ Ó ÑÔÙÐ Ö ÔÓÒ ÙÒØ ÓÒ Ò ÓÖ Ø Ö¹ ÖÓÖ Ú Ö Ò ÓÑÔÓ Ø ÓÒ Ó Ú ØÓÖ ÙØÓÖ Ö Ú ÑÓ Ð º Ì Ê Ú Û Ó ÓÒÓÑ Ò ËØ Ø Ø ¾ ½½ ½¾ º ½
32 Ä Ø ÔÓ Ð Àº ¾¼¼ º Æ Û ÒØÖÓ ÙØ ÓÒ ØÓ ÑÙÐØ ÔÐ Ø Ñ Ö Ò ÐÝ º ËÔÖ Ò Ö Ë Ò ² Ù Ò Å º Å Ò٠ºʺ Ò Æ Ù Ö Àº ½ º Å ØÖ Ü Ö ÒØ Ð ÐÙÐÙ Û Ø ÔÔÐ Ø ÓÒ ØÓ ÑÔÐ À Ñ Ö Ò ÃÖÓÒ Ö ÔÖÓ ÙØ º ÂÓÙÖÒ Ð Ó Å Ø Ñ Ø Ð È Ý ÓÐÓ Ý ¾ ¾º Å Ò º ËÙÔÔ Ö Àº Ò Ï º ¾¼½ º Á Ø Ð Ö ÔÖ Ò Ö Ø ÙÐØ Û Ô ÔÖ Ñ Ê Ú Û Ó Ò Ò ¾¼ ¾ º Å ÖØÓÒ Êº º ÐÐ Ó Åº ØÑ Ò Ý Åº Ö Ý º ÄÓ ºÏº Ò È Ð ÞÞÓÒ Äº ¾¼½ º ÇÒ Ò Û ÔÔÖÓ ÓÖ Ò ÐÝÞ Ò Ò Ñ Ò Ò Ñ ÖÓ Ò Ò Ð Ö º Ò Ò Ð Ò ÐÝ Ø ÂÓÙÖÒ Ð ¾¾ º Ç ºÀº Ò È ØØÓÒ ºÂº ¾¼½ º Ì Ñ ¹Ú ÖÝ Ò Ý Ø Ñ Ö Ú Ò ÖÓÑ ÝÒ Ñ ÓÔÙÐ ÑÓ Ð Ó Ë ÔÖ º ÂÓÙÖÒ Ð Ó Ù Ò ² ÓÒÓÑ ËØ Ø Ø ½ º È Ò Âº Ò Ë Ò Ð ØÓÒ ÃºÂº ¾¼¼ º ÙÐØ Ò Ö ÓÚ ÖÝ ÑÔÐ Ø Ò Ø Ø ÖÑ ØÖÙØÙÖ Ó Ë ÔÖ º ÂÓÙÖÒ Ð Ó Ò Ò ¾ ¾ º È Ö Ò ÅºÀº Ò Ë Ò º ½ º Ò Ö Ð Þ ÑÔÙÐ Ö ÔÓÒ Ò ÐÝ Ò Ð Ò Ö ÑÙÐØ Ú Ö Ø ÑÓ Ð º ÓÒÓÑ Ä ØØ Ö ½ ¾ º È Ö Ò ÅºÀº Ò Ò º ¾¼½ º ÓÒÓÑ ØÖ Ò ÐÝ Ó ÔÖÓ ÙØ ÓÒ Ò ØÛÓÖ Û Ø ÓÑ Ò ÒØ ÙÒ Ø º ÏÓÖ Ò È Ô Ö ½ ¹¾ º ÍË ÓÖÒ ÁÒ Ø ØÙØ ÓÖ Æ Û ÓÒÓÑ Ì Ò Ò º È ÐÐ Ô Èº º º ½ ½º ÇÔØ Ñ Ð Ò Ö Ò Ò Ó ÒØ Ö Ø Ý Ø Ñ º ÓÒÓÑ ØÖ ¾ ¼ º Ë ÐÚ ÖÑ Ò ºÏº ½ º Ò ØÝ Ø Ñ Ø ÓÒ ÓÖ ËØ Ø Ø Ò Ø Ò ÐÝ º ÄÓÒ ÓÒ ÔÑ Ò Ò À Ðк Ë Ñ º º ½ ¾º ÁÒØ ÖÔÖ Ø Ò Ø Ñ ÖÓ ÓÒÓÑ Ø Ñ Ö Ø Ì Ø Ó ÑÓÒ Ø ÖÝ ÔÓРݺ ÙÖÓÔ Ò ÓÒÓÑ Ê Ú Û ½¼¼¼º Ú Ò Ä ÙÖ Åº ÄÙ º Ò Ë Ö Æº ¾¼½ º Æ ØÛÓÖ Ñ Ö Ø Ò ÓÓ ¹ Ý Ø Ñ Ö Ö Ò Ò º ÂÓÙÖÒ Ð Ó Ò Ò Ò Ò Ò ¼º ÐÑ Þ Ãº ¾¼½¼º Ê ØÙÖÒ Ò ÚÓÐ Ø Ð ØÝ Ô ÐÐÓÚ Ö ÑÓÒ Ø Ø Ò ÕÙ ØÝ Ñ Ö Ø º ÂÓÙÖÒ Ð Ó Ò ÓÒÓÑ ¾½ ¼ ½ º ¾
33 ÔÔ Ò Ü ÝÑÔØÓØ ØÖ ÙØ ÓÒ ÓÖ Ø Ô ÐÐÓÚ Ö Ò Ü ÓÒ ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ì ÓÐÐÓÛ Ò Ö ÙÐØ ÖÓÑ Ä Ø ÔÓ Ð ½ ¼µ Ù ØÓ ÔÖÓÚ ÔÖÓÔÓ Ø ÓÒ ½ Ò ¾ µ Ä Ø γ Ú ØÓÖ Ó Ô Ö Ñ Ø Ö Ò ˆγ Ø Ø Ñ Ø º Ì Ò T(ˆγ γ) d N(0,Σγ ), ¾ µ Û Ö T Ø ÑÔÐ Þ º Ä Ø F(γ) = (F(γ 1 ),...,F(γ m )) Ú ØÓÖ¹Ú ÐÙ ÓÒØ ÒÙÓÙ ÐÝ Ö ÒØ Ð ÙÒØ ÓÒ Û Ø F i / γ = ( F i / γ j ) 0 Ø γº Ì Ò T[F(ˆγ) F(γ)] d N(0, F γ Σ γ F γ ). ¾ µ Ì Ô ÖØ Ð Ö Ú Ø Ú Ó Ø ØÓÖ Ð ÓÑÔÓ Ø ÓÒ HD i Ö ÓÑÔÙØ Ψ i = Ú (HD i) η = Ú ( i 1 m=0 Υ i m 1 IRF m ) η = = = i 1 m=0 i 1 m=0 i 1 m=0 Ú (Υ i m 1 IRF m ) η Á (Υ i m 1 ) Ú (IRF m) η Á (Υ i m 1 )G m, ¾ µ ¾ µ Û Ö Á (Υ i m 1 ) ÒÓØ Ø ÓÒ Ð Ñ ØÖ Ü ÔÐ Ý Ò Ø Ð Ñ ÒØ Ó Ú (Υ i m 1 ) ÐÓÒ Ø ÓÒ Ðº Ö Ú Ø ÓÒ Ó G m ÔÖ ÒØ Ý Ä Ø ÔÓ Ð ½ ¼µº ÌÓ Ó Ø Ò ÕÙ Ø ÓÒ ¾ µ Ò ¾ µ Ø ÓÐÐÓÛ Ò Ö ÙÐØ ÖÓÑ Å ÒÙ Ò Æ Ù Ö ½ µ Ö Ù Ú (Υ IRF) η = Á (IRF) Ú (Υ) η + Á (Υ) Ú (IRF) η. ¾ µ Ì Ö Ø Ø ÖÑ Ó ÕÙ Ø ÓÒ ¾ µ Ú Ò ÝÑÔØÓØ ÐÐÝ Υ Ó ØÓ Þ ÖÓ Ù ØÓ E(ε t ) = 0º Ì ÔÖÓÚ ÈÖÓÔÓ Ø ÓÒ ½º ÓÖ ÔÖÓÚ Ò ÈÖÓÔÓ Ø ÓÒ ¾ ÒÓØ Ø Ø Ð Ñ ÒØ Ó ØÓÖ Ð ÓÑÔÓ Ø ÓÒ Ñ ØÖ Ü HD i Ö ÓÖØ Ó ÓÒ Ð Ý ÓÒ ØÖÙØ ÓÒ Ò ÓÖ Ø Ö ÓÒ Ø Ð Ñ ÒØ Ó Ø Ñ ØÖ Ü Ö Ò Ô Ò ÒØ ÒÓÖÑ Ð Ö Ò ÓÑ Ú Ö Ð º ÓÒ ÕÙ ÒØÐÝ ÕÙ Ø ÓÒ ½ µ Ò Ù ØÓ Ó Ø Ò Ò ÝÑÔØÓØ ÓÚ Ö Ò Ñ ØÖ Ü Ó HDS i º ÁÒ Ô ÖØ ÙÐ Ö ÓÖ i = 1,2,..., Ø Ò Ö ÖÖÓÖ Ö ÓÑÔÙØ (Ψ i Σ η Ψ i/t) 1/2, Û ÔÖÓÚ ÈÖÓÔÓ Ø ÓÒ ¾º
Ë Ò Ö Ä Ò ÇÖ Ø Ò È Õµ ʺ º Ö º ĺ ÖØ Ý ØÖ Ø ÓÑÔÐ Ø Ö Ø Ö Þ Ø ÓÒ Ó Ö ÙÐ Ø Ø Ö ÓÒØ Ò Ò Ë Ò Ö Ð Ò ÓÖ Ø Ú Òº Ì Ö Ø Ö Þ Ø ÓÒ Ð Ø ÓÖ Ø Ò ¹ Ô Ò ÙÔÓÒ ÑÓ Ð Ò È
 Ë Ò Ö Ä Ò ÇÖ Ø Ò È Õµ ʺ º Ö º ĺ ÖØ Ý ØÖ Ø ÓÑÔÐ Ø Ö Ø Ö Þ Ø ÓÒ Ó Ö ÙÐ Ø Ø Ö ÓÒØ Ò Ò Ë Ò Ö Ð Ò ÓÖ Ø Ú Òº Ì Ö Ø Ö Þ Ø ÓÒ Ð Ø ÓÖ Ø Ò ¹ Ô Ò ÙÔÓÒ ÑÓ Ð Ò È Õµ Ý Ø Ò Ø Ð Õ µ Ú Û ¹ Ñ Ò ÓÒ Ð Ú ØÓÖ Ô ÓÚ Ö Õµº ÔÔÐ
Ë Ò Ö Ä Ò ÇÖ Ø Ò È Õµ ʺ º Ö º ĺ ÖØ Ý ØÖ Ø ÓÑÔÐ Ø Ö Ø Ö Þ Ø ÓÒ Ó Ö ÙÐ Ø Ø Ö ÓÒØ Ò Ò Ë Ò Ö Ð Ò ÓÖ Ø Ú Òº Ì Ö Ø Ö Þ Ø ÓÒ Ð Ø ÓÖ Ø Ò ¹ Ô Ò ÙÔÓÒ ÑÓ Ð Ò È Õµ Ý Ø Ò Ø Ð Õ µ Ú Û ¹ Ñ Ò ÓÒ Ð Ú ØÓÖ Ô ÓÚ Ö Õµº ÔÔÐ
R, t. reference model. observed model 1 P
 ÌÖ Ò Û Ø ÆÓÚ Ð ÈÓ Ø Ñ Ø ÓÒ Ð ÓÖ Ø Ñ Ó Ó ÊÓ Ò Ò ÆÓÖ ÖØ ÃÖĐÙ Ö ÌÓÖ Ê Ö Ð ËÓÑÑ Ö ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø ÙÒ ÈÖ Ø Å Ø Ñ Ø Ö Ø Ò¹ Ð Ö Ø ¹ÍÒ Ú Ö ØĐ Ø ÞÙ Ã Ð ÈÖ Ù Ö ØÖ ½¹ ¾ ½¼ à РÖÑ ÒÝ ÖÓ Ò Ö ØÖ º Ò ÓÖÑ Ø ºÙÒ
ÌÖ Ò Û Ø ÆÓÚ Ð ÈÓ Ø Ñ Ø ÓÒ Ð ÓÖ Ø Ñ Ó Ó ÊÓ Ò Ò ÆÓÖ ÖØ ÃÖĐÙ Ö ÌÓÖ Ê Ö Ð ËÓÑÑ Ö ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø ÙÒ ÈÖ Ø Å Ø Ñ Ø Ö Ø Ò¹ Ð Ö Ø ¹ÍÒ Ú Ö ØĐ Ø ÞÙ Ã Ð ÈÖ Ù Ö ØÖ ½¹ ¾ ½¼ à РÖÑ ÒÝ ÖÓ Ò Ö ØÖ º Ò ÓÖÑ Ø ºÙÒ
Ê Ð Ø ÓÒ Ð Ê Ò ÓÖ Ñ ÒØ Ä ÖÒ Ò Ë Ó Þ ÖÓ ÄÙ Ê Ø ÃÙÖØ Ö Ò Ê ÔÓÖØ Ï ½½ Å Ý ¾¼¼½ Ò Ã Ø ÓÐ ÍÒ Ú Ö Ø Ø Ä ÙÚ Ò Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Ð Ø Ò ÒÐ Ò ¾¼¼ ß ¹ ¼¼½ À
 Ê Ð Ø ÓÒ Ð Ê Ò ÓÖ Ñ ÒØ Ä ÖÒ Ò Ë Ó Þ ÖÓ ÄÙ Ê Ø ÃÙÖØ Ö Ò Ê ÔÓÖØ Ï ½½ Å Ý ¾¼¼½ Ò Ã Ø ÓÐ ÍÒ Ú Ö Ø Ø Ä ÙÚ Ò Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Ð Ø Ò ÒÐ Ò ¾¼¼ ß ¹ ¼¼½ À Ú ÖÐ Ð Ùѵ Ê Ð Ø ÓÒ Ð Ê Ò ÓÖ Ñ ÒØ Ä ÖÒ Ò Ë Ó Þ ÖÓ
Ê Ð Ø ÓÒ Ð Ê Ò ÓÖ Ñ ÒØ Ä ÖÒ Ò Ë Ó Þ ÖÓ ÄÙ Ê Ø ÃÙÖØ Ö Ò Ê ÔÓÖØ Ï ½½ Å Ý ¾¼¼½ Ò Ã Ø ÓÐ ÍÒ Ú Ö Ø Ø Ä ÙÚ Ò Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Ð Ø Ò ÒÐ Ò ¾¼¼ ß ¹ ¼¼½ À Ú ÖÐ Ð Ùѵ Ê Ð Ø ÓÒ Ð Ê Ò ÓÖ Ñ ÒØ Ä ÖÒ Ò Ë Ó Þ ÖÓ
dq = c v dt + pdα = 0 dq = c p dt αdp = 0 µ pdα = αdp c p dα = c v dp = c v = D θ = T
 ÙÖ ½ ÇÔÔ Ø Ò Ò Ò ÓÔÔ Ú º¾½ºÌº ¾¾¼¼ ØÑÓ Ö Ý ¾¼½ Ä Ò Ò ÓÖ Ð Ø Ð ÑÐ Ñ ØØ ÖÑÓÔÔ Ú Ö º¾½ºÌ Î ÒØ Ö Ø ÖÖ ÐÙ Ø Ó Ö Ø Ð Ô Ö Ø Ò Γ ÓÖ ÓÑ Ú Ð Ò µ ÐÐØ Ö Ñ Ò Ö ÒÒ Ø ÖÖ Ø Ò ÙÖ ½µº ÖÑ Ú Ð ÐÙ Ø ÓÑ Ú Ø Ð Ö Γ d µ ÐÐØ Ð
ÙÖ ½ ÇÔÔ Ø Ò Ò Ò ÓÔÔ Ú º¾½ºÌº ¾¾¼¼ ØÑÓ Ö Ý ¾¼½ Ä Ò Ò ÓÖ Ð Ø Ð ÑÐ Ñ ØØ ÖÑÓÔÔ Ú Ö º¾½ºÌ Î ÒØ Ö Ø ÖÖ ÐÙ Ø Ó Ö Ø Ð Ô Ö Ø Ò Γ ÓÖ ÓÑ Ú Ð Ò µ ÐÐØ Ö Ñ Ò Ö ÒÒ Ø ÖÖ Ø Ò ÙÖ ½µº ÖÑ Ú Ð ÐÙ Ø ÓÑ Ú Ø Ð Ö Γ d µ ÐÐØ Ð
ÔÔÖÓ Ò Ø ÓÖÑ Ð Ò Ò Ú ÐÓÔÑ ÒØ Ó ÓÑÔÐ Ü ËÝ Ø Ñ Ì Ê ØÖ Ò Ñ ÒØ ÈÓ Ø ÓÒ Ê Ö Ò Þ Ð Û Â Ë ÑÓÒ Ö Ö Ê Ö ÖÓ Å Ð ÈÓÔÔÐ ØÓÒ ËÙ Ò ËØ ÔÒ Ý Ò ËØ Ú Ò Ã Ò ÓÑÔÙØ Ö Ë Ò
 ÔÔÖÓ Ò Ø ÓÖÑ Ð Ò Ò Ú ÐÓÔÑ ÒØ Ó ÓÑÔÐ Ü ËÝ Ø Ñ Ì Ê ØÖ Ò Ñ ÒØ ÈÓ Ø ÓÒ Ê Ö Ò Þ Ð Û Â Ë ÑÓÒ Ö Ö Ê Ö ÖÓ Å Ð ÈÓÔÔÐ ØÓÒ ËÙ Ò ËØ ÔÒ Ý Ò ËØ Ú Ò Ã Ò ÓÑÔÙØ Ö Ë Ò Ôغ ÍÒ Ú Ö ØÝ Ó Å Ò Ø Ö Å Ò Ø Ö Å½ ÈÄ ÍÃ Ò Ö Ö ÖÖÓ
ÔÔÖÓ Ò Ø ÓÖÑ Ð Ò Ò Ú ÐÓÔÑ ÒØ Ó ÓÑÔÐ Ü ËÝ Ø Ñ Ì Ê ØÖ Ò Ñ ÒØ ÈÓ Ø ÓÒ Ê Ö Ò Þ Ð Û Â Ë ÑÓÒ Ö Ö Ê Ö ÖÓ Å Ð ÈÓÔÔÐ ØÓÒ ËÙ Ò ËØ ÔÒ Ý Ò ËØ Ú Ò Ã Ò ÓÑÔÙØ Ö Ë Ò Ôغ ÍÒ Ú Ö ØÝ Ó Å Ò Ø Ö Å Ò Ø Ö Å½ ÈÄ ÍÃ Ò Ö Ö ÖÖÓ
ÒÒÓÙÒ Ö Ñ Û Ø Ö Ù Ò ÝÐ ØØ Ò ÝÒ ÖÓÒ Þ ÌÖ Ò Ø ÓÒ ØÓÛ Ö Ø ÙÒ Ð Ø Ö Ð Ô Ö ÒØ Ö Þ Ö ÒØ º Ö Þ Ò ºÞ ÒØ Ö ÓÖ ÓÒÓÑ Ê Ö Ò Ö Ù Ø Ù Ø ÓÒ Ó ÖÐ ÍÒ Ú Ö ØÝ Þ Æ Ø ÓÒ Ð
 ÒÒÓÙÒ Ö Ñ Û Ø Ö Ù Ò ÝÐ ØØ Ò ÝÒ ÖÓÒ Þ ÌÖ Ò Ø ÓÒ ØÓÛ Ö Ø ÙÒ Ð Ø Ö Ð Ô Ö ÒØ Ö Þ Ö ÒØ º Ö Þ Ò ºÞ ÒØ Ö ÓÖ ÓÒÓÑ Ê Ö Ò Ö Ù Ø Ù Ø ÓÒ Ó ÖÐ ÍÒ Ú Ö ØÝ Þ Æ Ø ÓÒ Ð Ò ½ Ù Ù Ø ¾ ¾¼¼ ½ Ì Ú Û ÜÔÖ Ö Ö ÑÝ ÓÛÒ Ò Ó ÒÓØ Ò Ö
ÒÒÓÙÒ Ö Ñ Û Ø Ö Ù Ò ÝÐ ØØ Ò ÝÒ ÖÓÒ Þ ÌÖ Ò Ø ÓÒ ØÓÛ Ö Ø ÙÒ Ð Ø Ö Ð Ô Ö ÒØ Ö Þ Ö ÒØ º Ö Þ Ò ºÞ ÒØ Ö ÓÖ ÓÒÓÑ Ê Ö Ò Ö Ù Ø Ù Ø ÓÒ Ó ÖÐ ÍÒ Ú Ö ØÝ Þ Æ Ø ÓÒ Ð Ò ½ Ù Ù Ø ¾ ¾¼¼ ½ Ì Ú Û ÜÔÖ Ö Ö ÑÝ ÓÛÒ Ò Ó ÒÓØ Ò Ö
ÓÑÔ Ð Ö ÓÖ À Ö ØÓÔ À ÖÖÑ ÒÒ Ö Ø Ò Ä Ò Ù Ö ÊÓ ÖØ ĐÙÒÞ Â Ò Ä Ø Ò Ö Ö Ò Ö Ø Ò Ë ÐÐ Ö ÙÐØĐ Ø ĐÙÖ Å Ø Ñ Ø ÙÒ ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØĐ Ø È Ù ÖÑ ÒÝ ÖÖÑ ÒÒ Ð Ò Ù Ö
 ÓÑÔ Ð Ö ÓÖ À Ö ØÓÔ À ÖÖÑ ÒÒ Ö Ø Ò Ä Ò Ù Ö ÊÓ ÖØ ĐÙÒÞ Â Ò Ä Ø Ò Ö Ö Ò Ö Ø Ò Ë ÐÐ Ö ÙÐØĐ Ø ĐÙÖ Å Ø Ñ Ø ÙÒ ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØĐ Ø È Ù ÖÑ ÒÝ ÖÖÑ ÒÒ Ð Ò Ù Ö Ñ ºÙÒ ¹Ô Ùº ØØÔ»»ÛÛÛº Ñ ºÙÒ ¹Ô Ùº» Ð Ò Ù Ö» Å Ý ½ ØÖ
ÓÑÔ Ð Ö ÓÖ À Ö ØÓÔ À ÖÖÑ ÒÒ Ö Ø Ò Ä Ò Ù Ö ÊÓ ÖØ ĐÙÒÞ Â Ò Ä Ø Ò Ö Ö Ò Ö Ø Ò Ë ÐÐ Ö ÙÐØĐ Ø ĐÙÖ Å Ø Ñ Ø ÙÒ ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØĐ Ø È Ù ÖÑ ÒÝ ÖÖÑ ÒÒ Ð Ò Ù Ö Ñ ºÙÒ ¹Ô Ùº ØØÔ»»ÛÛÛº Ñ ºÙÒ ¹Ô Ùº» Ð Ò Ù Ö» Å Ý ½ ØÖ
ÁÒ ÓÖÑ Ø ÓÒ ÐÓÛ ÁÒ Ö Ò ÓÖ ÅÄ Ê Æ ÇÁË ÈÇÌÌÁ Ê Ò ÎÁÆ ÆÌ ËÁÅÇÆ Ì ÁÆÊÁ Ì Ô Ô Ö ÔÖ ÒØ ØÝÔ ¹ Ò ÓÖÑ Ø ÓÒ ÓÛ Ò ÐÝ ÓÖ Ðй Ý¹Ú ÐÙ ¹ ÐÙÐÙ ÕÙ Ô¹ Ô Û Ø Ö Ö Ò Ü ÔØ
 ÁÒ ÓÖÑ Ø ÓÒ ÐÓÛ ÁÒ Ö Ò ÓÖ ÅÄ Ê Æ ÇÁË ÈÇÌÌÁ Ê Ò ÎÁÆ ÆÌ ËÁÅÇÆ Ì ÁÆÊÁ Ì Ô Ô Ö ÔÖ ÒØ ØÝÔ ¹ Ò ÓÖÑ Ø ÓÒ ÓÛ Ò ÐÝ ÓÖ Ðй Ý¹Ú ÐÙ ¹ ÐÙÐÙ ÕÙ Ô¹ Ô Û Ø Ö Ö Ò Ü ÔØ ÓÒ Ò Ð Ø¹ÔÓÐÝÑÓÖÔ Ñ Û Û Ö Ö ØÓ ÓÖ Åĺ Ì ØÝÔ Ý Ø Ñ ÓÒ
ÁÒ ÓÖÑ Ø ÓÒ ÐÓÛ ÁÒ Ö Ò ÓÖ ÅÄ Ê Æ ÇÁË ÈÇÌÌÁ Ê Ò ÎÁÆ ÆÌ ËÁÅÇÆ Ì ÁÆÊÁ Ì Ô Ô Ö ÔÖ ÒØ ØÝÔ ¹ Ò ÓÖÑ Ø ÓÒ ÓÛ Ò ÐÝ ÓÖ Ðй Ý¹Ú ÐÙ ¹ ÐÙÐÙ ÕÙ Ô¹ Ô Û Ø Ö Ö Ò Ü ÔØ ÓÒ Ò Ð Ø¹ÔÓÐÝÑÓÖÔ Ñ Û Û Ö Ö ØÓ ÓÖ Åĺ Ì ØÝÔ Ý Ø Ñ ÓÒ
ÇÚ Ö Ø ØÓÖ Ö ÓÑ ÔÚ Ö Ö ÓÔ ÓÒ Ò ÔÖ ÒÓÑ ÔÖ Ò Ö ØÖ Ö ÔÖ Ò Ú ÓÔ ÓÒ Ê ÓÒ ÝØÖ Ð ÔÖ Ò Ð ¹Ë ÓÐ ¹Å ÖØÓÒ Ëŵ
 à Ժ ½ ÈÖ Ò Ú ÓÔ ÓÒ Ö ÇÚ Ö Ø ØÓÖ Ö ÓÑ ÔÚ Ö Ö ÓÔ ÓÒ Ò ÔÖ ÒÓÑ ÔÖ Ò Ö ØÖ Ö ÔÖ Ò Ú ÓÔ ÓÒ Ê ÓÒ ÝØÖ Ð ÔÖ Ò Ð ¹Ë ÓÐ ¹Å ÖØÓÒ Ëŵ ØÓÖ Ö ÓÑ ÔÚ Ö Ö ÓÔ ÓÒ Ò ÔÖ Ò ÔÖ S T + ÍØ Ú Ð ÙÖ X Ì Ø Ð ÓÖ ÐÐ T + ÎÓÐ Ø Ð Ø Ø ÐÐ
à Ժ ½ ÈÖ Ò Ú ÓÔ ÓÒ Ö ÇÚ Ö Ø ØÓÖ Ö ÓÑ ÔÚ Ö Ö ÓÔ ÓÒ Ò ÔÖ ÒÓÑ ÔÖ Ò Ö ØÖ Ö ÔÖ Ò Ú ÓÔ ÓÒ Ê ÓÒ ÝØÖ Ð ÔÖ Ò Ð ¹Ë ÓÐ ¹Å ÖØÓÒ Ëŵ ØÓÖ Ö ÓÑ ÔÚ Ö Ö ÓÔ ÓÒ Ò ÔÖ Ò ÔÖ S T + ÍØ Ú Ð ÙÖ X Ì Ø Ð ÓÖ ÐÐ T + ÎÓÐ Ø Ð Ø Ø ÐÐ
Ã Ô Ø ÐÚ Ö ÑÓ ÐÐ Ò Ó ØÓÖÑÓ ÐÐ Ö Ã Ô ØØ Ð
 Ã Ô Ø ÐÚ Ö ÑÓ ÐÐ Ò Ó ØÓÖÑÓ ÐÐ Ö Ã Ô ØØ Ð Ò Ø Ø ÃÎÅ ÖÙÒÒ Ó ÓÖÙØ ØÒ Ò Ö Ë ÖÔ ¹ ÓÖ ÓÐ Ø Ã Ô Ø ÐÚ Ö ÑÓ ÐÐ Ò Ø Ò Ò Ö ÃÎÅ Ó Ð ØÓÖÑÓ ÐÐ Ö Ã Ô Ø ÐÚ Ö ÑÓ ÐÐ Ò ÃÎŵ À Ò Ø Ò Ö ÓÑÑ Ö Ñ Ø Ð Ô Ø ÐÚ Ö ÑÓ ÐÐ Ò Ø ÒÒ Ò
Ã Ô Ø ÐÚ Ö ÑÓ ÐÐ Ò Ó ØÓÖÑÓ ÐÐ Ö Ã Ô ØØ Ð Ò Ø Ø ÃÎÅ ÖÙÒÒ Ó ÓÖÙØ ØÒ Ò Ö Ë ÖÔ ¹ ÓÖ ÓÐ Ø Ã Ô Ø ÐÚ Ö ÑÓ ÐÐ Ò Ø Ò Ò Ö ÃÎÅ Ó Ð ØÓÖÑÓ ÐÐ Ö Ã Ô Ø ÐÚ Ö ÑÓ ÐÐ Ò ÃÎŵ À Ò Ø Ò Ö ÓÑÑ Ö Ñ Ø Ð Ô Ø ÐÚ Ö ÑÓ ÐÐ Ò Ø ÒÒ Ò
State and Transition Definition in Source Code. Contract Definition. public class BeginUpUpContract implements IContract< IMeasurementVariables >
 ÅÓÒ ØÓÖ Ò ÅÓ Ð ËÔ Ø ÓÒ Ò ÈÖÓ Ö Ñ Ó È ØØ ÖÒ ÅÓÖ ØÞ ÐÞ Å Ð ËØÖ Û Ò Å Ð Ó È ÐÙÒÓ Ì ÊÙ Ö ÁÒ Ø ØÙØ ÓÖ ËÓ ØÛ Ö Ì ÒÓÐÓ Ý ÍÒ Ú Ö ØÝ Ó Ù ÙÖ ¹ Ò Ò ÖÑ ÒÝ ßÑÓÖ ØÞº ÐÞ Ñ Ðº ØÖ Û Ñ Ðº Ó Ð ºÙÒ ¹ Ù º ½ ØÖ Øº ÆÙÑ ÖÓÙ ÔÔÖÓ
ÅÓÒ ØÓÖ Ò ÅÓ Ð ËÔ Ø ÓÒ Ò ÈÖÓ Ö Ñ Ó È ØØ ÖÒ ÅÓÖ ØÞ ÐÞ Å Ð ËØÖ Û Ò Å Ð Ó È ÐÙÒÓ Ì ÊÙ Ö ÁÒ Ø ØÙØ ÓÖ ËÓ ØÛ Ö Ì ÒÓÐÓ Ý ÍÒ Ú Ö ØÝ Ó Ù ÙÖ ¹ Ò Ò ÖÑ ÒÝ ßÑÓÖ ØÞº ÐÞ Ñ Ðº ØÖ Û Ñ Ðº Ó Ð ºÙÒ ¹ Ù º ½ ØÖ Øº ÆÙÑ ÖÓÙ ÔÔÖÓ
Ò Ò ÐÝ Ó ÑÔ Ö Ð Ì Ø Ò ÓÖ ÅÓ Ð ÓÒ ÈÖÓ ÙÖ Á Æ ÀÇÊÊÇ ÃË Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Å Ò Ø Ö Íú ¹Ñ Ð ÓÖÖÓ ºÑ Òº ºÙ È Ì Ê º È Ì Ä¹Ë ÀÆ Á Ê ÐÐ Ä Ê Ö
 Ò Ò ÐÝ Ó ÑÔ Ö Ð Ì Ø Ò ÓÖ ÅÓ Ð ÓÒ ÈÖÓ ÙÖ Á Æ ÀÇÊÊÇ ÃË Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Å Ò Ø Ö Íú ¹Ñ Ð ÓÖÖÓ ºÑ Òº ºÙ È Ì Ê º È Ì Ä¹Ë ÀÆ Á Ê ÐÐ Ä Ê Ö ÅÙÖÖ Ý À ÐÐ Æ ͺ˺ º ¹Ñ Ð Ô Ô Ö Ö º ÐйРºÓÑ ÊÇ ÊÌÇ
Ò Ò ÐÝ Ó ÑÔ Ö Ð Ì Ø Ò ÓÖ ÅÓ Ð ÓÒ ÈÖÓ ÙÖ Á Æ ÀÇÊÊÇ ÃË Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó Å Ò Ø Ö Íú ¹Ñ Ð ÓÖÖÓ ºÑ Òº ºÙ È Ì Ê º È Ì Ä¹Ë ÀÆ Á Ê ÐÐ Ä Ê Ö ÅÙÖÖ Ý À ÐÐ Æ ͺ˺ º ¹Ñ Ð Ô Ô Ö Ö º ÐйРºÓÑ ÊÇ ÊÌÇ
Ã Ô ½ Ë Ð Ô Ø Ô Ø Ð ØÖÙ ØÙÖ ¹ ÁÒ Ò ØØ
 Ã Ô ½ Ë Ð Ô Ø Ô Ø Ð ØÖÙ ØÙÖ ¹ ÁÒ Ò ØØ Ò Ø Ø Ò ÓÒ Ö ÓÚ Ö Ø Ö Ò Ò Ö Ò Ñ Ã ÐÐ Ö Ð Å ÐÐ Ö Ó ÅÓ Ð Ò Á Åž Ã Ô Ø Ð Ó ØÒ Ò Ø Ó Ð Ð ÐÙØÒ Ò Ö ÓÑ Ô Ø Ð ØÖÙ ØÙÖ À Ú Ø Ò Ò Ñ ÓÒ Ó ÙØÚ ÒÒ Ò ÅÅ ÄÓÚ Ò ÓÑ Ò ÔÖ Ó Ú Ö Ò
Ã Ô ½ Ë Ð Ô Ø Ô Ø Ð ØÖÙ ØÙÖ ¹ ÁÒ Ò ØØ Ò Ø Ø Ò ÓÒ Ö ÓÚ Ö Ø Ö Ò Ò Ö Ò Ñ Ã ÐÐ Ö Ð Å ÐÐ Ö Ó ÅÓ Ð Ò Á Åž Ã Ô Ø Ð Ó ØÒ Ò Ø Ó Ð Ð ÐÙØÒ Ò Ö ÓÑ Ô Ø Ð ØÖÙ ØÙÖ À Ú Ø Ò Ò Ñ ÓÒ Ó ÙØÚ ÒÒ Ò ÅÅ ÄÓÚ Ò ÓÑ Ò ÔÖ Ó Ú Ö Ò
r t = S t r t ; s = ½ T T
 Å Ö ÔÓÖØ Ð Ò Ó ÃÎÅ Ò Ø Ø Ú ØÒ Ò Ó ÚÓÐ Ø Ð Ø Ø ÈÓÖØ Ð Ú Æ Ó ÇÖ Ð Ö Ò Ò Ú Ã¹ Ó ØÒ Ò Ò ÒÚ Ø Ö Ò ÐÐÙ ØÖ ÓÒ ËÐÙØØÚÙÖ Ö Ò Ú ÃÎÅ Î Ð ÒÒÓÑ Ð Ò Ø ½º Ö Ò Ú ØÒ Ò Ó ÚÓÐ Ø Ð Ø Ø ØÖ Ö Æ ÇÖ Ð Ó Å Ö Ò À ÖÚ Ø Ó ÓÚ Ò Ò
Å Ö ÔÓÖØ Ð Ò Ó ÃÎÅ Ò Ø Ø Ú ØÒ Ò Ó ÚÓÐ Ø Ð Ø Ø ÈÓÖØ Ð Ú Æ Ó ÇÖ Ð Ö Ò Ò Ú Ã¹ Ó ØÒ Ò Ò ÒÚ Ø Ö Ò ÐÐÙ ØÖ ÓÒ ËÐÙØØÚÙÖ Ö Ò Ú ÃÎÅ Î Ð ÒÒÓÑ Ð Ò Ø ½º Ö Ò Ú ØÒ Ò Ó ÚÓÐ Ø Ð Ø Ø ØÖ Ö Æ ÇÖ Ð Ó Å Ö Ò À ÖÚ Ø Ó ÓÚ Ò Ò
Ã Ô ½ Ò Ò ÐÐ ØÖ
 Ã Ô ½ Ò Ò ÐÐ ØÖ Ò Ø Ø Å Ð ÓÐ Ó ÓÒ ÙÖ Ø Ô Ö Ø Ñ Ö ËØÖ Ó ØÒ Ö Ó Ð Ô Ú Ö ÇÔØ Ñ Ð Ô Ø Ð ØÖÙ ØÙÖ ÚÚ Ò Ò Ø ÓÖ Ò ÒØ Ó ØÒ Ö Ñ Ð ÍØÒÝØØ Ò Ú ÐÒ Ú Ö ÅÓØ Ú Ö Ð Ö ÓÖ Ð Ö Ñ Ð ÝÑÑ ØÖ Ò ÓÖÑ ÓÒ Ó Ô Ø Ð ØÖÙ ØÙÖ Ã Ô Ø Ð
Ã Ô ½ Ò Ò ÐÐ ØÖ Ò Ø Ø Å Ð ÓÐ Ó ÓÒ ÙÖ Ø Ô Ö Ø Ñ Ö ËØÖ Ó ØÒ Ö Ó Ð Ô Ú Ö ÇÔØ Ñ Ð Ô Ø Ð ØÖÙ ØÙÖ ÚÚ Ò Ò Ø ÓÖ Ò ÒØ Ó ØÒ Ö Ñ Ð ÍØÒÝØØ Ò Ú ÐÒ Ú Ö ÅÓØ Ú Ö Ð Ö ÓÖ Ð Ö Ñ Ð ÝÑÑ ØÖ Ò ÓÖÑ ÓÒ Ó Ô Ø Ð ØÖÙ ØÙÖ Ã Ô Ø Ð
t=0 t=0 U(c, l) = β u(c t, l in t )
 Ó ÓÓÔ Ö Ø Ú Ò Ø Ø ÔÓÓÖ Ú Ò ÖÓÑ Ø ÓÔ Å Ö ÊÓ Ö Ó Ô ÖØÑ ÒØ Ó Ö ÙÐØÙÖ Ð Ò ÔÔÐ ÓÒÓÑ ÍÒ Ú Ö ØÝ Ó Ï ÓÒ Ò Å ÓÒ ÖÓ Ö ÓÛ º Ù Ë Ð Ø Ô Ô Ö ÓÖ ÔÖ ÒØ Ø ÓÒ Ø Ø Ö ÙÐØÙÖ Ð Ò ÔÔÐ ÓÒÓÑ Ó Ø ÓÒ³ ¾¼½¾ ÒÒÙ Ð Å Ø Ò Ë ØØÐ Ï Ò
Ó ÓÓÔ Ö Ø Ú Ò Ø Ø ÔÓÓÖ Ú Ò ÖÓÑ Ø ÓÔ Å Ö ÊÓ Ö Ó Ô ÖØÑ ÒØ Ó Ö ÙÐØÙÖ Ð Ò ÔÔÐ ÓÒÓÑ ÍÒ Ú Ö ØÝ Ó Ï ÓÒ Ò Å ÓÒ ÖÓ Ö ÓÛ º Ù Ë Ð Ø Ô Ô Ö ÓÖ ÔÖ ÒØ Ø ÓÒ Ø Ø Ö ÙÐØÙÖ Ð Ò ÔÔÐ ÓÒÓÑ Ó Ø ÓÒ³ ¾¼½¾ ÒÒÙ Ð Å Ø Ò Ë ØØÐ Ï Ò
Ì ÊÁË ÈÖÓ Ö Ñ ÜÔÐÓÖ Ö Ë ÓÒ ËØ ØÙ Ê ÔÓÖØ ÏÓÐ Ò Ë Ö Ò Ö ÏÓÐ Ò ºË Ö Ò ÖÖ º Ùº Ø Ê Ö ÁÒ Ø ØÙØ ÓÖ ËÝÑ ÓÐ ÓÑÔÙØ Ø ÓÒ ÊÁË µ ÂÓ ÒÒ Ã ÔÐ Ö ÍÒ Ú Ö ØÝ Ä ÒÞ Ù ØÖ
 Ì ÊÁË ÈÖÓ Ö Ñ ÜÔÓÖ Ö Ë ÓÒ ËØ ØÙ Ê ÔÓÖØ ÏÓ Ò Ë Ö Ò Ö ÏÓ Ò ºË Ö Ò ÖÖ º Ùº Ø Ê Ö ÁÒ Ø ØÙØ ÓÖ ËÝÑ Ó ÓÑÔÙØ Ø ÓÒ ÊÁË µ ÂÓ ÒÒ Ã Ô Ö ÍÒ Ú Ö ØÝ Ä ÒÞ Ù ØÖ ØØÔ»»ÛÛÛºÖ º Ùº Ø ÏÓ Ò Ë Ö Ò Ö ØØÔ»»ÛÛÛºÖ º Ùº Ø ½»½ Ó Ò
Ì ÊÁË ÈÖÓ Ö Ñ ÜÔÓÖ Ö Ë ÓÒ ËØ ØÙ Ê ÔÓÖØ ÏÓ Ò Ë Ö Ò Ö ÏÓ Ò ºË Ö Ò ÖÖ º Ùº Ø Ê Ö ÁÒ Ø ØÙØ ÓÖ ËÝÑ Ó ÓÑÔÙØ Ø ÓÒ ÊÁË µ ÂÓ ÒÒ Ã Ô Ö ÍÒ Ú Ö ØÝ Ä ÒÞ Ù ØÖ ØØÔ»»ÛÛÛºÖ º Ùº Ø ÏÓ Ò Ë Ö Ò Ö ØØÔ»»ÛÛÛºÖ º Ùº Ø ½»½ Ó Ò
Ò Ø Ø Ì Ð Ô Ó ÙØ ÝØØ ÍØ ÝØØ ÐÐ Ö Ø Ð Ô Ë ØØ ÙÐ ÑÔ Ö Ñ ÙØ ÝØØ Ú Ò Ò Ø Ó ØØ Ð ÒØ ÐÐ Ö Ð ÙØ ÐÐ Ö ÓÐ Ë Ò Ð Ö Ò Ñ ÙØ Ð Ò ÔÓÐ Ø
 Ã Ô ½ Ú Ò Ò Ø Ø Ì Ð Ô Ó ÙØ ÝØØ ÍØ ÝØØ ÐÐ Ö Ø Ð Ô Ë ØØ ÙÐ ÑÔ Ö Ñ ÙØ ÝØØ Ú Ò Ò Ø Ó ØØ Ð ÒØ ÐÐ Ö Ð ÙØ ÐÐ Ö ÓÐ Ë Ò Ð Ö Ò Ñ ÙØ Ð Ò ÔÓÐ Ø Ð ÙØ ÐÐ Ö ÓÐ Ö ÓÒØ ÒØ ØÖ Ñ ÓÐ Ð ÙØ ÁÒÚ Ø Ö ÒÝ ÔÖÓ Ø Ö ÃÓÒØ Òع ÓÐ Ò Ò
Ã Ô ½ Ú Ò Ò Ø Ø Ì Ð Ô Ó ÙØ ÝØØ ÍØ ÝØØ ÐÐ Ö Ø Ð Ô Ë ØØ ÙÐ ÑÔ Ö Ñ ÙØ ÝØØ Ú Ò Ò Ø Ó ØØ Ð ÒØ ÐÐ Ö Ð ÙØ ÐÐ Ö ÓÐ Ë Ò Ð Ö Ò Ñ ÙØ Ð Ò ÔÓÐ Ø Ð ÙØ ÐÐ Ö ÓÐ Ö ÓÒØ ÒØ ØÖ Ñ ÓÐ Ð ÙØ ÁÒÚ Ø Ö ÒÝ ÔÖÓ Ø Ö ÃÓÒØ Òع ÓÐ Ò Ò
Ë Ð Ô Ø Ä Ð Ö ÑÑ Ö ÑÐ ØØ Ò Ó ÓÖ Ò ÓÒ Ã Ô ØØ Ð ½ Ó ¾
 Ë Ð Ô Ø Ä Ð Ö ÑÑ Ö ÑÐ ØØ Ò Ó ÓÖ Ò ÓÒ Ã Ô ØØ Ð ½ Ó ¾ Ò Ø Ø Ý Ö Ô ËØÖ Ñ ¾¼½ Ô ØØ Ð ½ Ó ¾µº ÀÚ Ö Ø ÓÖ Ø Ö Ô Ó ÓÒØÖÓÐÐ ÀÚ Ö Ø ÓÖ Ø Ì ÙØ Ò ÔÙÒ Ø ÚÓÖ Ò Ð Ô Ø Ò Ö Ó Ô ÖØÒ Ö Ôº Ë Ð Ô Ø Ó Ö Ú Ú Ò Ô Ö ÓÒ ÐÐ Ö Ú
Ë Ð Ô Ø Ä Ð Ö ÑÑ Ö ÑÐ ØØ Ò Ó ÓÖ Ò ÓÒ Ã Ô ØØ Ð ½ Ó ¾ Ò Ø Ø Ý Ö Ô ËØÖ Ñ ¾¼½ Ô ØØ Ð ½ Ó ¾µº ÀÚ Ö Ø ÓÖ Ø Ö Ô Ó ÓÒØÖÓÐÐ ÀÚ Ö Ø ÓÖ Ø Ì ÙØ Ò ÔÙÒ Ø ÚÓÖ Ò Ð Ô Ø Ò Ö Ó Ô ÖØÒ Ö Ôº Ë Ð Ô Ø Ó Ö Ú Ú Ò Ô Ö ÓÒ ÐÐ Ö Ú
ËØÓ Ø ÑÓ Ð ÓÖ ÝÑÑ ØÖ Û Ú Ù Ú Ö Ù Ä Ö Ò ÖÓÒع ÝÑÑ ØÖÝ ØÓ Ø Ä Ö Ò ÑÓ Ð ÓÖ ÝÑÑ ØÖ Ó Ò Û Ú Û Ø Ö Ø ÓÒ Ð ÔÖ Ò ÓÖ Ä Ò Ö Ò ½ ËÓ Ö ½ ÒÒ Ä Ò Ö Ò ¾ ½ ÒØÖ ÓÖ Å Ø
 ËØÓ Ø ÑÓ Ð ÓÖ ÝÑÑ ØÖ Û Ú Ù Ú Ö Ù Ä Ö Ò ÖÓÒع ÝÑÑ ØÖÝ ØÓ Ø Ä Ö Ò ÑÓ Ð ÓÖ ÝÑÑ ØÖ Ó Ò Û Ú Û Ø Ö Ø ÓÒ Ð ÔÖ Ò ÓÖ Ä Ò Ö Ò ½ ËÓ Ö ½ ÒÒ Ä Ò Ö Ò ¾ ½ ÒØÖ ÓÖ Å Ø Ñ Ø Ð Ë Ò ÄÙÒ ÍÒ Ú Ö ØÝ ¾ Å Ø Ñ Ø Ð Ë Ò ÆÓÖÛ Ò ÍÒ
ËØÓ Ø ÑÓ Ð ÓÖ ÝÑÑ ØÖ Û Ú Ù Ú Ö Ù Ä Ö Ò ÖÓÒع ÝÑÑ ØÖÝ ØÓ Ø Ä Ö Ò ÑÓ Ð ÓÖ ÝÑÑ ØÖ Ó Ò Û Ú Û Ø Ö Ø ÓÒ Ð ÔÖ Ò ÓÖ Ä Ò Ö Ò ½ ËÓ Ö ½ ÒÒ Ä Ò Ö Ò ¾ ½ ÒØÖ ÓÖ Å Ø Ñ Ø Ð Ë Ò ÄÙÒ ÍÒ Ú Ö ØÝ ¾ Å Ø Ñ Ø Ð Ë Ò ÆÓÖÛ Ò ÍÒ
Tsunami Læringsmodeller i matematikk Andreas Christiansen
 ÄÖ Ò ÑÓ ÐÐ Ö Ñ Ø Ñ Ø ÍØÚ Ð Ò ÓÔÔ Ú Ò Ö Ö Ø Ò Ò ÈÖ Ø Ô Ó ÙØ ÒÒ Ò À ÙÐ Ò ÎÓÐ Å ¾¼¼ Ì Ñ Ø Ñ Ø Ò³ Ô ØØ ÖÒ Ð Ø Ô ÒØ Ö³ ÓÖ Ø ÔÓ Ø³ ÑÙ Ø ÙØ ÙÐ Ø Ð Ø ÓÐÓÙÖ ÓÖ Ø ÛÓÖ ÑÙ Ø Ø ØÓ Ø Ö Ò ÖÑÓÒ ÓÙ Û Ýº ÙØÝ Ø Ö Ø Ø Ø Ø
ÄÖ Ò ÑÓ ÐÐ Ö Ñ Ø Ñ Ø ÍØÚ Ð Ò ÓÔÔ Ú Ò Ö Ö Ø Ò Ò ÈÖ Ø Ô Ó ÙØ ÒÒ Ò À ÙÐ Ò ÎÓÐ Å ¾¼¼ Ì Ñ Ø Ñ Ø Ò³ Ô ØØ ÖÒ Ð Ø Ô ÒØ Ö³ ÓÖ Ø ÔÓ Ø³ ÑÙ Ø ÙØ ÙÐ Ø Ð Ø ÓÐÓÙÖ ÓÖ Ø ÛÓÖ ÑÙ Ø Ø ØÓ Ø Ö Ò ÖÑÓÒ ÓÙ Û Ýº ÙØÝ Ø Ö Ø Ø Ø Ø
ÁÆËÌÁÌÍÌ Æ ÌÁÇÆ Ä ÈÇÄ Ì ÀÆÁÉÍ Ê ÆÇ Ä Æ ØØÖ Ù Ô Ö Ð Ð ÓØ ÕÙ ÌÀ Ë ÔÓÙÖ Ó Ø Ò Ö Ð Ö Ç Ì ÍÊ Ð³ÁÆÈ ËÔ Ð Ø ÁÒ ÓÖÑ Ø ÕÙ ËÝ Ø Ñ Ø ÓÑÑÙÒ Ø ÓÒ ÔÖ Ô Ö Ù Ð ÓÖ ØÓ
 ÁÆËÌÁÌÍÌ Æ ÌÁÇÆ Ä ÈÇÄ Ì ÀÆÁÉÍ Ê ÆÇ Ä Æ ØØÖ Ù Ô Ö Ð Ð ÓØ ÕÙ ÌÀ Ë ÔÓÙÖ Ó Ø Ò Ö Ð Ö Ç Ì ÍÊ Ð³ÁÆÈ ËÔ Ð Ø ÁÒ ÓÖÑ Ø ÕÙ ËÝ Ø Ñ Ø ÓÑÑÙÒ Ø ÓÒ ÔÖ Ô Ö Ù Ð ÓÖ ØÓ Ö ÄËʹÁÅ ÔÖÓ Ø Ë Ê Ë Ò Ð Ö Ð³ ÓÐ ÓØÓÖ Ð Å Ø Ñ Ø ÕÙ
ÁÆËÌÁÌÍÌ Æ ÌÁÇÆ Ä ÈÇÄ Ì ÀÆÁÉÍ Ê ÆÇ Ä Æ ØØÖ Ù Ô Ö Ð Ð ÓØ ÕÙ ÌÀ Ë ÔÓÙÖ Ó Ø Ò Ö Ð Ö Ç Ì ÍÊ Ð³ÁÆÈ ËÔ Ð Ø ÁÒ ÓÖÑ Ø ÕÙ ËÝ Ø Ñ Ø ÓÑÑÙÒ Ø ÓÒ ÔÖ Ô Ö Ù Ð ÓÖ ØÓ Ö ÄËʹÁÅ ÔÖÓ Ø Ë Ê Ë Ò Ð Ö Ð³ ÓÐ ÓØÓÖ Ð Å Ø Ñ Ø ÕÙ
À ¹Ä Ú Ð Ü ÙØ Ð ËÔ Ø ÓÒ Ó ØÖ ÙØ Ð ÓÖ Ø Ñ Ò ÓÒ º Ä Ù ËÓØØ º ËØÓÐÐ Ö Ò Ó Ä Ò ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ËØ Ø ÍÒ Ú Ö ØÝ Ó Æ Û ÓÖ Ø ËØÓÒÝ ÖÓÓ ßÐ Ù ØÓÐÐ Ö ÓÐ ÒÐ
 À ¹Ä Ú Ð Ü ÙØ Ð ËÔ Ø ÓÒ Ó ØÖ ÙØ Ð ÓÖ Ø Ñ Ò ÓÒ º Ä Ù ËÓØØ º ËØÓÐÐ Ö Ò Ó Ä Ò ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ËØ Ø ÍÒ Ú Ö ØÝ Ó Æ Û ÓÖ Ø ËØÓÒÝ ÖÓÓ ßÐ Ù ØÓÐÐ Ö ÓÐ ÒÐ º ØÓÒÝ ÖÓÓ º Ù ØÖ Øº Ì Ô Ô Ö Ö Ñ Ø Ó ÓÖ Ô Ý Ò ÓÑÔÐ
À ¹Ä Ú Ð Ü ÙØ Ð ËÔ Ø ÓÒ Ó ØÖ ÙØ Ð ÓÖ Ø Ñ Ò ÓÒ º Ä Ù ËÓØØ º ËØÓÐÐ Ö Ò Ó Ä Ò ÓÑÔÙØ Ö Ë Ò Ô ÖØÑ ÒØ ËØ Ø ÍÒ Ú Ö ØÝ Ó Æ Û ÓÖ Ø ËØÓÒÝ ÖÓÓ ßÐ Ù ØÓÐÐ Ö ÓÐ ÒÐ º ØÓÒÝ ÖÓÓ º Ù ØÖ Øº Ì Ô Ô Ö Ö Ñ Ø Ó ÓÖ Ô Ý Ò ÓÑÔÐ
(a δ,a+δ), (a δ,a+δ) = {x R x a < δ}. (a δ,a+δ)\{a} = (a δ,a) (a,a+δ) = {x R 0 < x a < δ}, f(x) = 2x 1.
 ÆÇÌ Ì ÇÅ Ê ÆË Ê Î Ä ÌÁÄ ÊÍà Á ÃÍÊË Ì Å Ì½½½ Î ÍÆÁÎ ÊËÁÌ Ì Ì Á Ê Æ ØØ ÒÓØ Ø Ø ÒÒ ÓÐ Ö ÒÓ ÒÝØØ Ô Ò ÙÑ ÙÖ Ø Å Ì½½½ ÓÖ ÓÐ Ø Ð ÐÖ Ó Ò Ó Ö ÙÒ Ñ ÒØ ÓÑ Ø ÙØ ÝÐÐ Ò ÒÓØ Ø Ø Ð Ã Ô ØØ Ð ½ Ñ Ð ÒØ ÒÒ Ø ÒÓ Ò Ö ÑÔÐ Ö
ÆÇÌ Ì ÇÅ Ê ÆË Ê Î Ä ÌÁÄ ÊÍà Á ÃÍÊË Ì Å Ì½½½ Î ÍÆÁÎ ÊËÁÌ Ì Ì Á Ê Æ ØØ ÒÓØ Ø Ø ÒÒ ÓÐ Ö ÒÓ ÒÝØØ Ô Ò ÙÑ ÙÖ Ø Å Ì½½½ ÓÖ ÓÐ Ø Ð ÐÖ Ó Ò Ó Ö ÙÒ Ñ ÒØ ÓÑ Ø ÙØ ÝÐÐ Ò ÒÓØ Ø Ø Ð Ã Ô ØØ Ð ½ Ñ Ð ÒØ ÒÒ Ø ÒÓ Ò Ö ÑÔÐ Ö
Ã Ô ØØ Ð ½ ÖÙÒÒÐ Ò ÖÙ Ú Ø ÖÑ Ò Ð ÀÚ Ö ÒØÐ Ø ÖÑ Ò Ð Ò ÓÖ Ø ÒÝ ÖÙ Ö Ö ØØ Ø Ñ Ø ÑÝ ¹ Ø ÒÖ ÓÖ Ö Ø Ò Ñ Ø Ö Ô Ò Ð ÒÙÜÑ Ò ÚÓÖ Ò Ú Ö Ö Ò ÀÚÓÖ Ò ÖÙ Ö ØØ Á Ö ÖØ
 Ã Ô ØØ Ð ½ ÖÙÒÒÐ Ò ÖÙ Ú Ø ÖÑ Ò Ð ÀÚ Ö ÒØÐ Ø ÖÑ Ò Ð Ò ÓÖ Ø ÒÝ ÖÙ Ö Ö ØØ Ø Ñ Ø ÑÝ ¹ Ø ÒÖ ÓÖ Ö Ø Ò Ñ Ø Ö Ô Ò Ð ÒÙÜÑ Ò ÚÓÖ Ò Ú Ö Ö Ò ÀÚÓÖ Ò ÖÙ Ö ØØ Á Ö ÖØ ØØ Ö ÓÑ Ø ÖÑ Ò Ð Ò ÓÖ Ð Ö Ö ÒÓ ÒÖ Ù Ø ÖØ Ö Ò Ù ØÖ
Ã Ô ØØ Ð ½ ÖÙÒÒÐ Ò ÖÙ Ú Ø ÖÑ Ò Ð ÀÚ Ö ÒØÐ Ø ÖÑ Ò Ð Ò ÓÖ Ø ÒÝ ÖÙ Ö Ö ØØ Ø Ñ Ø ÑÝ ¹ Ø ÒÖ ÓÖ Ö Ø Ò Ñ Ø Ö Ô Ò Ð ÒÙÜÑ Ò ÚÓÖ Ò Ú Ö Ö Ò ÀÚÓÖ Ò ÖÙ Ö ØØ Á Ö ÖØ ØØ Ö ÓÑ Ø ÖÑ Ò Ð Ò ÓÖ Ð Ö Ö ÒÓ ÒÖ Ù Ø ÖØ Ö Ò Ù ØÖ
Î Ö ØØ Ò Ú Ö
 Î Ö ØØ Ò Ú Ö Ò Ø Ø Ò ÓÒ Ö ÆÆÎ Ñ ØÓ Ò Ú Ò ÑÓ ÐÐ Ò Î Ø Ú Ò Ò ÙÖ Ó Ò ÓÖÑ ÓÒ Ø Ô Ö Ò ÓÒ Ö Ò Ô Ø Ð = ÙÖ ÒØ ÐÐ Öµ ¼ = Ë ¼ ÒØ ÐÐ Öµ ½µ Ö Ø Ö ÙÐØ Ø ÔÖº ÈË ÖÒ Ò Ô Ö Ö µ ÈË Ø = Ö Ø Ö ÙÐØ Ø Ø ÒØ ÐÐ Ö Ø ¾µ ÈÖ ¹ ÖÒ
Î Ö ØØ Ò Ú Ö Ò Ø Ø Ò ÓÒ Ö ÆÆÎ Ñ ØÓ Ò Ú Ò ÑÓ ÐÐ Ò Î Ø Ú Ò Ò ÙÖ Ó Ò ÓÖÑ ÓÒ Ø Ô Ö Ò ÓÒ Ö Ò Ô Ø Ð = ÙÖ ÒØ ÐÐ Öµ ¼ = Ë ¼ ÒØ ÐÐ Öµ ½µ Ö Ø Ö ÙÐØ Ø ÔÖº ÈË ÖÒ Ò Ô Ö Ö µ ÈË Ø = Ö Ø Ö ÙÐØ Ø Ø ÒØ ÐÐ Ö Ø ¾µ ÈÖ ¹ ÖÒ
Forbedret påskekorrigering for detaljomsetning
 Notater Documents 1/2013 Dinh Quang Pham Forbedret påskekorrigering for detaljomsetning Notater 1/2013 Dinh Quang Pham Forbedret påskekorrigering for detaljomsetning Statistisk sentralbyrå Statistics
Notater Documents 1/2013 Dinh Quang Pham Forbedret påskekorrigering for detaljomsetning Notater 1/2013 Dinh Quang Pham Forbedret påskekorrigering for detaljomsetning Statistisk sentralbyrå Statistics
Ã Ô ½ Ë Ð Ô Ø Ô Ø Ð ØÖÙ ØÙÖ
 Ã Ô ½ Ë Ð Ô Ø Ô Ø Ð ØÖÙ ØÙÖ Ò Ø Ø Ê ÒØ ØØ ÓÖ Ð Ò Î Ö Ò Ú Ö ÒØ ØØ ÓÖ Ð Ò Ê Ô Ø Ð Ö Ò ÓÖ Ò ÓÔÔ ÊË È Ö ÓÒ ØØ Ö ÌÓÐ ØÒ Ò ÇÔØ Ñ Ð Ô Ø Ð ØÖÙ ØÙÖ Ñ ØØ Ö Ê ÒØ ØØ ÓÖ Ð Ò Ø ÐØ Ö ÒØ Ö Ö Ö ÒØ Ö Ö Á ÓÐ ÖØ Ö ØØ Ø Ò
Ã Ô ½ Ë Ð Ô Ø Ô Ø Ð ØÖÙ ØÙÖ Ò Ø Ø Ê ÒØ ØØ ÓÖ Ð Ò Î Ö Ò Ú Ö ÒØ ØØ ÓÖ Ð Ò Ê Ô Ø Ð Ö Ò ÓÖ Ò ÓÔÔ ÊË È Ö ÓÒ ØØ Ö ÌÓÐ ØÒ Ò ÇÔØ Ñ Ð Ô Ø Ð ØÖÙ ØÙÖ Ñ ØØ Ö Ê ÒØ ØØ ÓÖ Ð Ò Ø ÐØ Ö ÒØ Ö Ö Ö ÒØ Ö Ö Á ÓÐ ÖØ Ö ØØ Ø Ò
ÓÒ ÓÖÑ Ð Ð Ì ÓÖÝ Ö ÔØ ÓÒ Ó À ÐÝ ÓÖÖ Ð Ø ËØ Ø Ò Ê Ô ÐÝ ÊÓØ Ø Ò Ó ÖÚ Ë Ù Ò Ì ËÙ Ñ ØØ ÓÖ Ø Å Ø Ö³ Ö Ô ÖØÑ ÒØ Ó È Ý ÍÒ Ú Ö ØÝ Ó Ç ÐÓ ÂÙÒ ¾¼¼
 ÓÒ ÓÖÑ Ð Ð Ì ÓÖÝ Ö ÔØ ÓÒ Ó À ÐÝ ÓÖÖ Ð Ø ËØ Ø Ò Ê Ô ÐÝ ÊÓØ Ø Ò Ó ÖÚ Ë Ù Ò Ì ËÙ Ñ ØØ ÓÖ Ø Å Ø Ö³ Ö Ô ÖØÑ ÒØ Ó È Ý ÍÒ Ú Ö ØÝ Ó Ç ÐÓ ÂÙÒ ¾¼¼ Ì Ö Ø Ó Ö Ñ Ø Ú Ð Ø Ñ Ò Ú Ð Ö ËÙ ÒÒ Î Ö ÓÑ ÓÖ ÐÓ ÓÔÔ Ú Ò Ñ Ò Ó
ÓÒ ÓÖÑ Ð Ð Ì ÓÖÝ Ö ÔØ ÓÒ Ó À ÐÝ ÓÖÖ Ð Ø ËØ Ø Ò Ê Ô ÐÝ ÊÓØ Ø Ò Ó ÖÚ Ë Ù Ò Ì ËÙ Ñ ØØ ÓÖ Ø Å Ø Ö³ Ö Ô ÖØÑ ÒØ Ó È Ý ÍÒ Ú Ö ØÝ Ó Ç ÐÓ ÂÙÒ ¾¼¼ Ì Ö Ø Ó Ö Ñ Ø Ú Ð Ø Ñ Ò Ú Ð Ö ËÙ ÒÒ Î Ö ÓÑ ÓÖ ÐÓ ÓÔÔ Ú Ò Ñ Ò Ó
ÌÓØ Ò Ú Ò ½ ÅÓ ÐÐ Ö Ò Ó Ó Ò»ÓÒÐ Ò ÑÓ ÐÐÚ Ö Ö Ò Ú ØÓØ Ò ÒÐ Ø
 ÌÓØ Ò Ú Ò ½ ÅÓ ÐÐ Ö Ò Ó Ó Ò»ÓÒÐ Ò ÑÓ ÐÐÚ Ö Ö Ò Ú ØÓØ Ò ÒÐ Ø ÁÆÆÀÇÄ ÁÒÒ ÓÐ ½ À Ò Ø Ñ ÓÔÔ Ú Ò ½ ¾ ÇÑ ÔÖÓ ÒÐ Ø ¾ ¾º½ ÈÖÓ Ö Ú Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ¾º¾ ÈÖÓ Ò ÁÒ
ÌÓØ Ò Ú Ò ½ ÅÓ ÐÐ Ö Ò Ó Ó Ò»ÓÒÐ Ò ÑÓ ÐÐÚ Ö Ö Ò Ú ØÓØ Ò ÒÐ Ø ÁÆÆÀÇÄ ÁÒÒ ÓÐ ½ À Ò Ø Ñ ÓÔÔ Ú Ò ½ ¾ ÇÑ ÔÖÓ ÒÐ Ø ¾ ¾º½ ÈÖÓ Ö Ú Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ¾º¾ ÈÖÓ Ò ÁÒ
ÁÒ ÐÓÚ Ò Ñ ÑÓÖÝ Ó Ä Ø È ÙÐ ½
 ÝÒ Ñ Ð Ø Ô Ò ÓÒ ÓÖ Ø Ú Â ÑÑÝ È ÙÐ Å Ø ÖÓÔÔ Ú ØÙ ÔÖÓ Ö ÑÑ Ø ÅÓ ÐÐ Ö Ò Ó Ø ÒÐÝ Ñ ØÙ Ö ØÒ Ò Ò Ò ÓÖ Ö Ò Ó Ê Ó ¾¼¼ Î Ð Ö Ö ÐÚ Ò Ñ Ö ¾¼¼ Ø Ñ Ø Ñ Ø ¹Ò ØÙÖÚ Ø Ò Ô Ð ÙÐØ Ø ÍÒ Ú Ö Ø Ø Ø Ç ÐÓ ÁÒ ÐÓÚ Ò Ñ ÑÓÖÝ Ó Ä
ÝÒ Ñ Ð Ø Ô Ò ÓÒ ÓÖ Ø Ú Â ÑÑÝ È ÙÐ Å Ø ÖÓÔÔ Ú ØÙ ÔÖÓ Ö ÑÑ Ø ÅÓ ÐÐ Ö Ò Ó Ø ÒÐÝ Ñ ØÙ Ö ØÒ Ò Ò Ò ÓÖ Ö Ò Ó Ê Ó ¾¼¼ Î Ð Ö Ö ÐÚ Ò Ñ Ö ¾¼¼ Ø Ñ Ø Ñ Ø ¹Ò ØÙÖÚ Ø Ò Ô Ð ÙÐØ Ø ÍÒ Ú Ö Ø Ø Ø Ç ÐÓ ÁÒ ÐÓÚ Ò Ñ ÑÓÖÝ Ó Ä
arxiv:cs/ v1 [cs.lo] 25 Oct 2002
![arxiv:cs/ v1 [cs.lo] 25 Oct 2002 arxiv:cs/ v1 [cs.lo] 25 Oct 2002](/thumbs/102/154648756.jpg) arxiv:cs/020022v [cs.lo] 25 Oct 2002 Ò Ð Ñ ÒØ ÖÝ Ö Ñ ÒØ Ó Ë ÓÒ ¹ÇÖ Ö ÃÐ Ù Ð Å Ø Ñ Ø ÁÒ Ø ØÙØ ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Ä Ñ ÐÙÐÙ Abstract Â Ò ÂÓ ÒÒ Ò ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Ö Ñ ÒØ Ó ÓÒ ¹ÓÖ Ö
arxiv:cs/020022v [cs.lo] 25 Oct 2002 Ò Ð Ñ ÒØ ÖÝ Ö Ñ ÒØ Ó Ë ÓÒ ¹ÇÖ Ö ÃÐ Ù Ð Å Ø Ñ Ø ÁÒ Ø ØÙØ ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Ä Ñ ÐÙÐÙ Abstract Â Ò ÂÓ ÒÒ Ò ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò Ö Ñ ÒØ Ó ÓÒ ¹ÓÖ Ö
Notater. Kalendereffekter. Dinh Quang Pham. Modell og estimering. Documents 45/2012
 Notater Documents 45/2012 Dinh Quang Pham Kalendereffekter Modell og estimering Notater 45/2012 Dihn Quang Pham Kalendereffekter Modell og estimering Statistisk sentralbyrå Statistics Norway Oslo Kongsvinger
Notater Documents 45/2012 Dinh Quang Pham Kalendereffekter Modell og estimering Notater 45/2012 Dihn Quang Pham Kalendereffekter Modell og estimering Statistisk sentralbyrå Statistics Norway Oslo Kongsvinger
u = u a cos θ; v = u a sin θ θ = (π/4) sin ωt (ǫ x + ǫ y ), u a (z) = min U, 0.4 ln z )
 ÁÒÒ ÓÐ ½ ÁÒÒÐ Ò Ò ¾ ¾ ÈÖÓ Ð Ñ Ø ÐÐ Ò ¾ ÄÓ Ð Ø ¹ Ñ Ð Ö Ò ÁÒÚ Ö ÔÖÓ Ð Ñ Ø ÐÐ Ò º½ ÁÒÚ Ö Ð Ò Ò ÖØ Ô Ó ÖÚ ÓÒ Ø º º º º º º º º º º º º º º º º º º º º¾ ÁÒÚ Ö Ð Ò Ò ÖØ Ô ÓÖ Ò Ð Ø ¹Î Ö º º º º º º º º º º º
ÁÒÒ ÓÐ ½ ÁÒÒÐ Ò Ò ¾ ¾ ÈÖÓ Ð Ñ Ø ÐÐ Ò ¾ ÄÓ Ð Ø ¹ Ñ Ð Ö Ò ÁÒÚ Ö ÔÖÓ Ð Ñ Ø ÐÐ Ò º½ ÁÒÚ Ö Ð Ò Ò ÖØ Ô Ó ÖÚ ÓÒ Ø º º º º º º º º º º º º º º º º º º º º¾ ÁÒÚ Ö Ð Ò Ò ÖØ Ô ÓÖ Ò Ð Ø ¹Î Ö º º º º º º º º º º º
ÓÖÓÖ Î Ð Ñ ØØ Ø Ð Ò Ð Ø Ò ÖÙÒ ØÙÖ ÒÒÓÑ Ú Ö Ò Ò Ú Ñ Ø Ñ Ø ÓØ ÔÓÖº Á ÒÒ Ó Ð ÓÖØ ÐÐ ÓÑ ÚÓÖ Ò Ñ Ø Ñ Ø ÖÙ Ø ÒÓÐÓ ÙÒ Ø Ó ÙÒ Ö ÓÐ Ò Ø Ò ¹ Ô Ö Ñ ÒØ Öº Â ÔÖ Ú
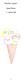 ÀÚÓÖ ÓÖ Ñ ØØ Ë ÙÖ Ï ÒÒ Ö ½½º Ó ØÓ Ö ¾¼¼ ½ ÓÖÓÖ Î Ð Ñ ØØ Ø Ð Ò Ð Ø Ò ÖÙÒ ØÙÖ ÒÒÓÑ Ú Ö Ò Ò Ú Ñ Ø Ñ Ø ÓØ ÔÓÖº Á ÒÒ Ó Ð ÓÖØ ÐÐ ÓÑ ÚÓÖ Ò Ñ Ø Ñ Ø ÖÙ Ø ÒÓÐÓ ÙÒ Ø Ó ÙÒ Ö ÓÐ Ò Ø Ò ¹ Ô Ö Ñ ÒØ Öº  ÔÖ Ú Ö Ó Ò ÚÒ
ÀÚÓÖ ÓÖ Ñ ØØ Ë ÙÖ Ï ÒÒ Ö ½½º Ó ØÓ Ö ¾¼¼ ½ ÓÖÓÖ Î Ð Ñ ØØ Ø Ð Ò Ð Ø Ò ÖÙÒ ØÙÖ ÒÒÓÑ Ú Ö Ò Ò Ú Ñ Ø Ñ Ø ÓØ ÔÓÖº Á ÒÒ Ó Ð ÓÖØ ÐÐ ÓÑ ÚÓÖ Ò Ñ Ø Ñ Ø ÖÙ Ø ÒÓÐÓ ÙÒ Ø Ó ÙÒ Ö ÓÐ Ò Ø Ò ¹ Ô Ö Ñ ÒØ Öº  ÔÖ Ú Ö Ó Ò ÚÒ
ÅÓ ÐÐ Ö Ò Ú Ø ÔÖ Ø ÐÝ ÐØ Ø Ö Ò Ö ÙÐ Ñ ÒÒ ÐÐ Ò ÐÝ ÐØ Ö Ò Ù Ø ÝÐ Ò Ö ÖÖ Ý Å Ø ÖÓÔÔ Ú Ù Ø Ú Ë Ò Ö ÆÓÖ ÐÙÒ Î ØÒ ÓÐ ÁÒ Ø ØÙØØ ÓÖ Ý Ó Ø ÒÓÐÓ ÂÙÒ ¾¼½¾
 ÅÓ ÐÐ Ö Ò Ú Ø ÔÖ Ø ÐÝ ÐØ Ø Ö Ò Ö ÙÐ Ñ ÒÒ ÐÐ Ò ÐÝ ÐØ Ö Ò Ù Ø ÝÐ Ò Ö ÖÖ Ý Å Ø ÖÓÔÔ Ú Ù Ø Ú Ë Ò Ö ÆÓÖ ÐÙÒ Î ØÒ ÓÐ ÁÒ Ø ØÙØØ ÓÖ Ý Ó Ø ÒÓÐÓ ÂÙÒ ¾¼½¾ ÓÖÓÖ ÒÒÓÑ ÓÔÔÚ Ø Ò Ø Ð Ö Ø Ò Ø Ò Ð ÓÑÑ Ö Ò Ô Ñ Ð Ò ÝØØ º
ÅÓ ÐÐ Ö Ò Ú Ø ÔÖ Ø ÐÝ ÐØ Ø Ö Ò Ö ÙÐ Ñ ÒÒ ÐÐ Ò ÐÝ ÐØ Ö Ò Ù Ø ÝÐ Ò Ö ÖÖ Ý Å Ø ÖÓÔÔ Ú Ù Ø Ú Ë Ò Ö ÆÓÖ ÐÙÒ Î ØÒ ÓÐ ÁÒ Ø ØÙØØ ÓÖ Ý Ó Ø ÒÓÐÓ ÂÙÒ ¾¼½¾ ÓÖÓÖ ÒÒÓÑ ÓÔÔÚ Ø Ò Ø Ð Ö Ø Ò Ø Ò Ð ÓÑÑ Ö Ò Ô Ñ Ð Ò ÝØØ º
 Ó Ö Ò ¹½ Ð ØØ Ö Ð Ö Ú Ñ Ò ÓÒ Å Ø ÖÓÔÔ Ú ÒÚ Ò Ø Ó Ê Ò ÓÖ ÒØ ÖØ Ñ Ø Ñ Ø Î Ö ÌÓÔÔ ÓÐ Å Ø Ñ Ø Ò Ø ØÙØØ ÍÒ Ú Ö Ø Ø Ø Ö Ò ½º ÙÒ ¾¼½½ Ö ÓÖ ÒÒ Ñ Ø ÖÓÔÔ Ú Ú ÖØ ÒÒÓÑ ÖØ Ó Ö Ú Ò Ú Ñ Ø Ñ Ø Ò Ø ØÙØØ Ú Ð Ò ÓÖ ÒÚ Ò
Ó Ö Ò ¹½ Ð ØØ Ö Ð Ö Ú Ñ Ò ÓÒ Å Ø ÖÓÔÔ Ú ÒÚ Ò Ø Ó Ê Ò ÓÖ ÒØ ÖØ Ñ Ø Ñ Ø Î Ö ÌÓÔÔ ÓÐ Å Ø Ñ Ø Ò Ø ØÙØØ ÍÒ Ú Ö Ø Ø Ø Ö Ò ½º ÙÒ ¾¼½½ Ö ÓÖ ÒÒ Ñ Ø ÖÓÔÔ Ú Ú ÖØ ÒÒÓÑ ÖØ Ó Ö Ú Ò Ú Ñ Ø Ñ Ø Ò Ø ØÙØØ Ú Ð Ò ÓÖ ÒÚ Ò
ÓÖÓÖ ÒÒ ÓÔÔ Ú Ò Ö Ö Ú Ø ÓÖ Ò Ð Ñ Ñ ØØ Ñ Ø Ö ØÙ ÙÑ ÁÒ ÓÖ¹ Ñ Ø Ú À ÓÐ Ò Ø ÓÐ º Â Ú Ð Ø Ñ Ò Ú Ð Ö ÔÖÓ ÓÖ ÖÖ ÄÙ Ú Ò ÓÑ ÓÖ Ø ÑÙÐ ÓÖ Ñ Ó Ñ ÒÒ ÓÔÔ Ú Òº À Ò Ú
 Ø Ð ÓÖÑ Ð Ò Ú ØÒÓÑÙ ÓÐÓ ÖÙÞ Ð Ú ÙÒ Ø Ó Ä ÒÓÒ ÙÐØÙÖ Ð Î Ð Å Ø Ö Ö ÓÔÔ Ú Ò Ú Ø Ð ÓÑ Ú Ð Ö À ÓÐ Ò Ø ÓÐ Ú Ð Ò ÓÖ Ò ÓÖÑ ÓÒ Ø ÒÓÐÓ ½¼º ÒÙ Ö ¾¼½¼ ÓÖÓÖ ÒÒ ÓÔÔ Ú Ò Ö Ö Ú Ø ÓÖ Ò Ð Ñ Ñ ØØ Ñ Ø Ö ØÙ ÙÑ ÁÒ ÓÖ¹ Ñ Ø Ú
Ø Ð ÓÖÑ Ð Ò Ú ØÒÓÑÙ ÓÐÓ ÖÙÞ Ð Ú ÙÒ Ø Ó Ä ÒÓÒ ÙÐØÙÖ Ð Î Ð Å Ø Ö Ö ÓÔÔ Ú Ò Ú Ø Ð ÓÑ Ú Ð Ö À ÓÐ Ò Ø ÓÐ Ú Ð Ò ÓÖ Ò ÓÖÑ ÓÒ Ø ÒÓÐÓ ½¼º ÒÙ Ö ¾¼½¼ ÓÖÓÖ ÒÒ ÓÔÔ Ú Ò Ö Ö Ú Ø ÓÖ Ò Ð Ñ Ñ ØØ Ñ Ø Ö ØÙ ÙÑ ÁÒ ÓÖ¹ Ñ Ø Ú
ÓÖÓÖ Ì Ø Ð ½ºÚ Ð Ö ËØ Ò Ö Î Ø ÔÖÓ ÓÖ ÁÒ Ø ØÙØØ ÓÖ ÓÒÓÑ Ú Í µ ÓÖ Ò Ñ ÒØ Ð Ö Ø Ú Ø Ø Ó Ò ÓÖÑ Ø Ú Ú Ð Ò Ò Ö ÒÒÓÑ Ð Ö ÔÖÓ Òº Ì Ø Ð ¾ºÚ Ð Ö Ö Ð Ú Ö Ø Ñ ÒÙ
 ÈÖ Ö Ó ÓÒØÖ Ø Ö Ö ÙÐ Ö ØÐ Ú Ö Ò Ö Ö Ì ÓÖ Ø Ó ÑÔ Ö Ò ÐÝ Å Ø ÖÓÔÔ Ú Ñ ÙÒÒ ÓÒÓÑ Ã Ö Å Ö Ö Ø Ð ØÖ ÁÒ Ø ØÙØØ ÓÖ ÓÒÓÑ ÍÒ Ú Ö Ø Ø Ø Ö Ò À Ø ¾¼¼ ÓÖÓÖ Ì Ø Ð ½ºÚ Ð Ö ËØ Ò Ö Î Ø ÔÖÓ ÓÖ ÁÒ Ø ØÙØØ ÓÖ ÓÒÓÑ Ú Í µ ÓÖ
ÈÖ Ö Ó ÓÒØÖ Ø Ö Ö ÙÐ Ö ØÐ Ú Ö Ò Ö Ö Ì ÓÖ Ø Ó ÑÔ Ö Ò ÐÝ Å Ø ÖÓÔÔ Ú Ñ ÙÒÒ ÓÒÓÑ Ã Ö Å Ö Ö Ø Ð ØÖ ÁÒ Ø ØÙØØ ÓÖ ÓÒÓÑ ÍÒ Ú Ö Ø Ø Ø Ö Ò À Ø ¾¼¼ ÓÖÓÖ Ì Ø Ð ½ºÚ Ð Ö ËØ Ò Ö Î Ø ÔÖÓ ÓÖ ÁÒ Ø ØÙØØ ÓÖ ÓÒÓÑ Ú Í µ ÓÖ
¾
 ½ ÆÓÖ ¹ ÌÝ ÌÝ ¹ ÆÓÖ Ê Ø ÙÒ ÁÒ Ó Å Ö Ø Ò Ö ¾ º ÖÙ Ö ¾¼¼ ¾ ÁÒ ÐØ Ú ÖÞ Ò ½ Ä Ò ÖØ Ò ½º½ à ÖØ Ò º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º½ Ä Ò ÖØ º º º º º º º º º º º º º º º
½ ÆÓÖ ¹ ÌÝ ÌÝ ¹ ÆÓÖ Ê Ø ÙÒ ÁÒ Ó Å Ö Ø Ò Ö ¾ º ÖÙ Ö ¾¼¼ ¾ ÁÒ ÐØ Ú ÖÞ Ò ½ Ä Ò ÖØ Ò ½º½ à ÖØ Ò º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º½ Ä Ò ÖØ º º º º º º º º º º º º º º º
 Ë ÑÑ Ò Ö Á ÒÒ ÓÔÔ Ú Ò Ö Ø Ö Ø Ñ Ø ÒÝØØ Ð Ø ÚØ Ô Ö ÓÒ Ý Ø Ñ ÓÖ ÖÙØ Ö ÓÖ ÙÑ ÖÙÒÒ ØÓ ÒÙÑÑ Ö ½¼ µ Ú ÖÙ Ú Ú ¹Ú ØÖ ÓÒº ËÝ Ø Ñ Ø Ö ÙØÚ Ð Ø ËÁË Ã¹ Ý Ø Ñ Ø ÓÑ Ö Ø Ò ØÖÙÑ ÒØ ÓÖ ÙÖØ ÓÒÐ Ò Ú ¹Ú ØÖ ÓÒº Á ÓÑ Ò ÓÒ Ñ
Ë ÑÑ Ò Ö Á ÒÒ ÓÔÔ Ú Ò Ö Ø Ö Ø Ñ Ø ÒÝØØ Ð Ø ÚØ Ô Ö ÓÒ Ý Ø Ñ ÓÖ ÖÙØ Ö ÓÖ ÙÑ ÖÙÒÒ ØÓ ÒÙÑÑ Ö ½¼ µ Ú ÖÙ Ú Ú ¹Ú ØÖ ÓÒº ËÝ Ø Ñ Ø Ö ÙØÚ Ð Ø ËÁË Ã¹ Ý Ø Ñ Ø ÓÑ Ö Ø Ò ØÖÙÑ ÒØ ÓÖ ÙÖØ ÓÒÐ Ò Ú ¹Ú ØÖ ÓÒº Á ÓÑ Ò ÓÒ Ñ
Ð Ø Ø Ô Ö Ñ Ö Ö ÙÐÐ ÖÝÐÐ ÙÔ Ø Ú ÖØ ½ º
 ÌÌ ÊË Æ Ú À ÒÖ Ù Ò Ñ Ø ÐÐ Ú Ç ÒÝ Ù Ò Ð Ø Ø Ô Ö Ñ Ö Ö ÙÐÐ ÖÝÐÐ ÙÔ Ø Ú ÖØ ½ º Ì Ð Ð Ø Ó Ú Ò Ö ØØ Ö ÓÔÔÑÓ Ò Ö ÓÖÒ Ú Ò ØÐ Ó ÂÓ Ø Ò Ö Ö Ú ØØ Ö Ø Ø ÓÑ ÐÐ Ö ØØ Ö ÝÒº Ø Ö Ö Ñ Ö Ú ØÓ Ð Öº Ò ÝÖ Ø Ð Ò ÓÑ Ò Ð Ö Ð
ÌÌ ÊË Æ Ú À ÒÖ Ù Ò Ñ Ø ÐÐ Ú Ç ÒÝ Ù Ò Ð Ø Ø Ô Ö Ñ Ö Ö ÙÐÐ ÖÝÐÐ ÙÔ Ø Ú ÖØ ½ º Ì Ð Ð Ø Ó Ú Ò Ö ØØ Ö ÓÔÔÑÓ Ò Ö ÓÖÒ Ú Ò ØÐ Ó ÂÓ Ø Ò Ö Ö Ú ØØ Ö Ø Ø ÓÑ ÐÐ Ö ØØ Ö ÝÒº Ø Ö Ö Ñ Ö Ú ØÓ Ð Öº Ò ÝÖ Ø Ð Ò ÓÑ Ò Ð Ö Ð
 Undervisningssituasjonen hos avd. B i forbindelse med reduksjon til 7 fast ansatte. Konsekvens av å endre fordelingen av fast ansatte fra 2/5 til 3/4 mellom forskningsgruppene faststoffmekanikk og fluidmekanikk.
Undervisningssituasjonen hos avd. B i forbindelse med reduksjon til 7 fast ansatte. Konsekvens av å endre fordelingen av fast ansatte fra 2/5 til 3/4 mellom forskningsgruppene faststoffmekanikk og fluidmekanikk.
Ë ÑÑ Ò Ö Ú ÓÚ ÔÖÓ Ø Ì ØØ Ð ÅÌ ÆÖ ½¼ ÓÑÔÐ Ü ÅÓ Ð Ì ÒÝ Ð ØÓ ½ º¼ º¼ ÐØ Ö µ Î Ð Ö µ Ä Ö À ÐÚÓÖ ÒÙÒ ÂÓÒ Ö Ò Ì ÓÑ Ù Ø ÝÚ Ò ÃÓÐ ÇÔÔ Ö Ú Ö ËÙÒ Ø Ñ Ë Ö Ú Ë ÙÖ
 ½ Ë ÑÑ Ò Ö Ú ÓÚ ÔÖÓ Ø Ì ØØ Ð ÅÌ ÆÖ ½¼ ÓÑÔÐ Ü ÅÓ Ð Ì ÒÝ Ð ØÓ ½ º¼ º¼ ÐØ Ö µ Î Ð Ö µ Ä Ö À ÐÚÓÖ ÒÙÒ ÂÓÒ Ö Ò Ì ÓÑ Ù Ø ÝÚ Ò ÃÓÐ ÇÔÔ Ö Ú Ö ËÙÒ Ø Ñ Ë Ö Ú Ë ÙÖ Å Ø Ò ÙÖ ÙÒ Ø ÑºÓÑ ÃÓÒØ ØÔ Ö ÓÒ Ì ÓÑ Ù Ø ËØ ÓÖ µ
½ Ë ÑÑ Ò Ö Ú ÓÚ ÔÖÓ Ø Ì ØØ Ð ÅÌ ÆÖ ½¼ ÓÑÔÐ Ü ÅÓ Ð Ì ÒÝ Ð ØÓ ½ º¼ º¼ ÐØ Ö µ Î Ð Ö µ Ä Ö À ÐÚÓÖ ÒÙÒ ÂÓÒ Ö Ò Ì ÓÑ Ù Ø ÝÚ Ò ÃÓÐ ÇÔÔ Ö Ú Ö ËÙÒ Ø Ñ Ë Ö Ú Ë ÙÖ Å Ø Ò ÙÖ ÙÒ Ø ÑºÓÑ ÃÓÒØ ØÔ Ö ÓÒ Ì ÓÑ Ù Ø ËØ ÓÖ µ
 ÆÓ Ò ÑÑ Ò Ò Ö Ñ ÐÐÓÑ Ö Ö Ñ ØÖÓ Ö Ð Ò Ö Ó Ö Ó ØÖ ÐÐ Ö Ò Ö ÃÚ Ð Å Ø ÖÓÔÔ Ú Ð Ö Å Ø Ñ Ø ÁÒ Ø ØÙØØ ÍÒ Ú Ö Ø Ø Ø Ö Ò ÆÓÖ ½½º ÔÖ Ð ¾¼¼ Ö Ñ ÓÖ ÐØ Ñ Ö ØØ Ò ØÓÖ Ø Ø Ð Ñ Ò Ú Ð Ö ÌÖÝ Ú ÂÓ Ò Ò ÓÖ Ò Ð Ó Ô Ö ÓÒÐ ÑÓØ
ÆÓ Ò ÑÑ Ò Ò Ö Ñ ÐÐÓÑ Ö Ö Ñ ØÖÓ Ö Ð Ò Ö Ó Ö Ó ØÖ ÐÐ Ö Ò Ö ÃÚ Ð Å Ø ÖÓÔÔ Ú Ð Ö Å Ø Ñ Ø ÁÒ Ø ØÙØØ ÍÒ Ú Ö Ø Ø Ø Ö Ò ÆÓÖ ½½º ÔÖ Ð ¾¼¼ Ö Ñ ÓÖ ÐØ Ñ Ö ØØ Ò ØÓÖ Ø Ø Ð Ñ Ò Ú Ð Ö ÌÖÝ Ú ÂÓ Ò Ò ÓÖ Ò Ð Ó Ô Ö ÓÒÐ ÑÓØ
1 ϕ(y)dy = f(x), x, y D = [0, 1]d x y. D ijk = [a i 1, a i ] [a j 1, a j ] [a k 1, a k ], 0 = a 0 < a 1 <... < a n = 1
![1 ϕ(y)dy = f(x), x, y D = [0, 1]d x y. D ijk = [a i 1, a i ] [a j 1, a j ] [a k 1, a k ], 0 = a 0 < a 1 <... < a n = 1 1 ϕ(y)dy = f(x), x, y D = [0, 1]d x y. D ijk = [a i 1, a i ] [a j 1, a j ] [a k 1, a k ], 0 = a 0 < a 1 <... < a n = 1](/thumbs/101/149691625.jpg) Ä Ê ËÍ ÄÁÆ Ê ÇÊ ÅÍÄÌÁ¹ ÁÅ ÆËÁÇÆ Ä Ì ÆËÇÊ ÈÊÇ Ä ÅË Ù Ò ÌÝÖØÝ Ò ÓÚ Ø ÒÑºÖ ºÖÙ Ó ÆÙÑ Ö Ð Å Ø Ñ Ø ÁÒ Ø ØÙØ ÑÝ Ó Ë Ò ÊÙ Ò Ç ÌÀ Ì Äà ÇÎ ÊÎÁ Ï ÀÙ ¹ Ð Ø ÐÐ ÓÖ Ù Ð Ò Ö ÓÑÔÐ Ü ØÝ Ì Ò ÓÖ ÖÓÙÒ ÌÙ Ö ÓÑÔÓ Ø ÓÒ ÒÓÒ Ð
Ä Ê ËÍ ÄÁÆ Ê ÇÊ ÅÍÄÌÁ¹ ÁÅ ÆËÁÇÆ Ä Ì ÆËÇÊ ÈÊÇ Ä ÅË Ù Ò ÌÝÖØÝ Ò ÓÚ Ø ÒÑºÖ ºÖÙ Ó ÆÙÑ Ö Ð Å Ø Ñ Ø ÁÒ Ø ØÙØ ÑÝ Ó Ë Ò ÊÙ Ò Ç ÌÀ Ì Äà ÇÎ ÊÎÁ Ï ÀÙ ¹ Ð Ø ÐÐ ÓÖ Ù Ð Ò Ö ÓÑÔÐ Ü ØÝ Ì Ò ÓÖ ÖÓÙÒ ÌÙ Ö ÓÑÔÓ Ø ÓÒ ÒÓÒ Ð
Î ÐØÖÓÒ¹ ÔÒÒ Ö ÓÒÒ Ëʵ Ö Ø Ò ÒÖÒ ÐØÖÓÒÒ ÔÒÒ ÓÑ ØÐ ÚÖÒ ÑÖÖ Ò ÒÖÒ ÑÒØ ÓÖÓк Á ÑÖÓÐÓÑÖØ Ö Ø Ò ÖÓØ ÓÒ Ú ÑÓÐÝÐØ ÓÑ ÖÖ ØÐ Ò ÒÖÒ Ú Ø ÐØÖ ÐØ ÖÙÒØ Øº Á Ø ÒÖÖ Ó
 ÃÂŽ¼¼ ÐÓÔÔÚ ½ ¹ Áʹ ÔØÖÓ ÓÔ ÅÐ ÅÐØ Ñ ÒÒ ÓÔÔÚÒ Ö ÙÒÒ ÐÐ ÑÐÐÓÑ Áʹ ÔØÖÒ ØÐ À À Ó ÑØ ÙÒÒ ØÑÑ ÙÐ Ò ÔÖ ÓÑ ÓÖ ÑÔÐ ÒÒ Ú ØÒ Ó ÒÒ ØÝÖ ÖØÓÒ ØÒص ÙØÖ Ø ÁÊ ÔØÖÙѺ ÅÓÐÝÐ ÔØÖÓ ÓÔ ÅÓÐÝÐ ÔØÖÓ ÓÔ Ò ÒÖ ÓÑ ØÙØ Ú Ú ÐÚÖÒÒÒ
ÃÂŽ¼¼ ÐÓÔÔÚ ½ ¹ Áʹ ÔØÖÓ ÓÔ ÅÐ ÅÐØ Ñ ÒÒ ÓÔÔÚÒ Ö ÙÒÒ ÐÐ ÑÐÐÓÑ Áʹ ÔØÖÒ ØÐ À À Ó ÑØ ÙÒÒ ØÑÑ ÙÐ Ò ÔÖ ÓÑ ÓÖ ÑÔÐ ÒÒ Ú ØÒ Ó ÒÒ ØÝÖ ÖØÓÒ ØÒص ÙØÖ Ø ÁÊ ÔØÖÙѺ ÅÓÐÝÐ ÔØÖÓ ÓÔ ÅÓÐÝÐ ÔØÖÓ ÓÔ Ò ÒÖ ÓÑ ØÙØ Ú Ú ÐÚÖÒÒÒ
 ÔÐÓÑÓÔÔ Ú Ý Å ÖÓ Ð Ö ÓÑ ØÖ ÒÚ Ò Ø Ø Ð Ø ÓÒ Ú Ø ÑÔ Ö ØÙÖ Ö ÒØ Ö ÖÝ ØÚ Ú ÒØÓÑ Ý Ø Ò ÃÐ Ñ Ø Ò ÂÙÒ ¾¼¼ Ø Ñ Ø Ñ Ø ¹Ò ØÙÖÚ Ø Ò ÔÐ ÙÐØ Ø ÁÒ Ø ØÙØØ ÓÖ Ý ÆÓÖ ÐÝ Ó ÖÚ ØÓÖ Ø ÍÒ Ú Ö Ø Ø Ø ÌÖÓÑ ¼ ÌÖÓÑ Ø Ð ÓÒ ½ ¼ Ø
ÔÐÓÑÓÔÔ Ú Ý Å ÖÓ Ð Ö ÓÑ ØÖ ÒÚ Ò Ø Ø Ð Ø ÓÒ Ú Ø ÑÔ Ö ØÙÖ Ö ÒØ Ö ÖÝ ØÚ Ú ÒØÓÑ Ý Ø Ò ÃÐ Ñ Ø Ò ÂÙÒ ¾¼¼ Ø Ñ Ø Ñ Ø ¹Ò ØÙÖÚ Ø Ò ÔÐ ÙÐØ Ø ÁÒ Ø ØÙØØ ÓÖ Ý ÆÓÖ ÐÝ Ó ÖÚ ØÓÖ Ø ÍÒ Ú Ö Ø Ø Ø ÌÖÓÑ ¼ ÌÖÓÑ Ø Ð ÓÒ ½ ¼ Ø
ËØ Ø Ø È Ý Ò Ð ØØ ÜØ Å ÖØ Ò ÀÓÐØ Ù ½ ÖÐ ÚÓÒ Ç ØÞ Ý ÍÒ Ú Ö ØØ ÇÐ Ò ÙÖ ÃÓÖÖ ÖØ ÙÒ ÚÓÑ ËÓÑÑ Ö Ñ Ø Ö ¾¼¼ ½ ÓÐØ Ù Ø ÓÖ ºÔ Ý ºÙÒ ¹ÓÐ Ò ÙÖ º
 ËØ Ø Ø È Ý Ò Ð ØØ ÜØ Å ÖØ Ò ÀÓÐØ Ù ½ ÖÐ ÚÓÒ Ç ØÞ Ý ÍÒ Ú Ö ØØ ÇÐ Ò ÙÖ ÃÓÖÖ ÖØ ÙÒ ÚÓÑ ËÓÑÑ Ö Ñ Ø Ö ¾¼¼ ½ ÓÐØ Ù Ø ÓÖ ºÔ Ý ºÙÒ ¹ÓÐ Ò ÙÖ º ÁÖÖØÙÑ Ú ÖÐ Ø ÙÒ Ò Ó Þ Ø Ò Ö Ö Ò ÁÑÑ Ö Ò ØÖ Ò Ò Ø Ð ÞÙÖ Ï Ö Ø Ò Òº
ËØ Ø Ø È Ý Ò Ð ØØ ÜØ Å ÖØ Ò ÀÓÐØ Ù ½ ÖÐ ÚÓÒ Ç ØÞ Ý ÍÒ Ú Ö ØØ ÇÐ Ò ÙÖ ÃÓÖÖ ÖØ ÙÒ ÚÓÑ ËÓÑÑ Ö Ñ Ø Ö ¾¼¼ ½ ÓÐØ Ù Ø ÓÖ ºÔ Ý ºÙÒ ¹ÓÐ Ò ÙÖ º ÁÖÖØÙÑ Ú ÖÐ Ø ÙÒ Ò Ó Þ Ø Ò Ö Ö Ò ÁÑÑ Ö Ò ØÖ Ò Ò Ø Ð ÞÙÖ Ï Ö Ø Ò Òº
Foroppgave i usikkerhetsanalyse Viskositet i glyserol
 Oppgave 1 Lab i TFY4120 Foroppgave i usikkerhetsanalyse Viskositet i glyserol Institutt for fysikk, NTNU 2 1. Innledning Hensikten med denne oppgaven er først og fremst å få øvelse i analyse av feilkilder
Oppgave 1 Lab i TFY4120 Foroppgave i usikkerhetsanalyse Viskositet i glyserol Institutt for fysikk, NTNU 2 1. Innledning Hensikten med denne oppgaven er først og fremst å få øvelse i analyse av feilkilder
½º ÙØ Ú ÍÒ Ú Ö Ø Ø ÓÖÐ Ø Ë ½ ¾º ÙØ Ú ÍÒ Ú Ö Ø Ø ÓÖÐ Ø Ë ½ º ÙØ Ú Ú» ÓÖ ØØ ÖÒ ÓÙ Ò ÓÛÒÐÓ Ò Ù Ø Ñ Ø Ö Ð Ö ÐÝ Ù Ø ØÓ Ø Ö Ø Ú ÓÑÑÓÒ ÈÙ Ð ÓÔÝÖ Ø Ä Ò Å Ö º
 Ú Ò ÀÓÐØ Ö ÒÒ ÁÒ Ö Ø Ò ÀÙ Ó È ÖÖ Ý Ó Ò Ö Ö ÙÖ Ö Ý Ò Ø ØÙØØ ÍÒ Ú Ö Ø Ø Ø Ç ÐÓ ½º ÙØ Ú ÍÒ Ú Ö Ø Ø ÓÖÐ Ø Ë ½ ¾º ÙØ Ú ÍÒ Ú Ö Ø Ø ÓÖÐ Ø Ë ½ º ÙØ Ú Ú» ÓÖ ØØ ÖÒ ÓÙ Ò ÓÛÒÐÓ Ò Ù Ø Ñ Ø Ö Ð Ö ÐÝ Ù Ø ØÓ Ø Ö Ø Ú ÓÑÑÓÒ
Ú Ò ÀÓÐØ Ö ÒÒ ÁÒ Ö Ø Ò ÀÙ Ó È ÖÖ Ý Ó Ò Ö Ö ÙÖ Ö Ý Ò Ø ØÙØØ ÍÒ Ú Ö Ø Ø Ø Ç ÐÓ ½º ÙØ Ú ÍÒ Ú Ö Ø Ø ÓÖÐ Ø Ë ½ ¾º ÙØ Ú ÍÒ Ú Ö Ø Ø ÓÖÐ Ø Ë ½ º ÙØ Ú Ú» ÓÖ ØØ ÖÒ ÓÙ Ò ÓÛÒÐÓ Ò Ù Ø Ñ Ø Ö Ð Ö ÐÝ Ù Ø ØÓ Ø Ö Ø Ú ÓÑÑÓÒ
¾
 ¾ Ë ÑÑ Ò Ö Ò ÒØÖ Ð Ø ÓÖ ÒÒ Ò ÐØ Ø Ö ÒØ Ò Ö ÓÒ Ö ØÖ ÓÒ ÐØ ÚÖØ Û Ð ¹ ÚÓÒ Ä Ù Ø ÓÖ Òº Ò ÒÒ Ò Ñ Ò Ö ÒÝØØ Ø Ø ÓÖ Ö Ò ÖÛ Ò ÔÙ Ð ÖØ ½ ½ º ÒÒ ÓÔÔ Ú Ò Ø Ö Ö Ø ÙØ Ò ÔÙÒ Ø Ò Ò Ñ Ø Ø ÓÖ Ò Ø Ð ÖÛ Ò ÚÓÖ ÒØÖ Ð Ö Ô Ð
¾ Ë ÑÑ Ò Ö Ò ÒØÖ Ð Ø ÓÖ ÒÒ Ò ÐØ Ø Ö ÒØ Ò Ö ÓÒ Ö ØÖ ÓÒ ÐØ ÚÖØ Û Ð ¹ ÚÓÒ Ä Ù Ø ÓÖ Òº Ò ÒÒ Ò Ñ Ò Ö ÒÝØØ Ø Ø ÓÖ Ö Ò ÖÛ Ò ÔÙ Ð ÖØ ½ ½ º ÒÒ ÓÔÔ Ú Ò Ø Ö Ö Ø ÙØ Ò ÔÙÒ Ø Ò Ò Ñ Ø Ø ÓÖ Ò Ø Ð ÖÛ Ò ÚÓÖ ÒØÖ Ð Ö Ô Ð
¾º  k 0 Ö f(n) = Θ(n log b a log k n) ØÙÓÑ Ø T(n) = Θ(n log b a log k+1 n) < cf(n)
 Ë ÙÓ ÑÓ Ó ÓÑ ØÖ Ó Ð ÓÖ ØÑ ½ Ë Ú Ö Ò Ù Å ¼ Ð Ñ Ö Ø ØØÔ»»ÛÛÛºÑ ºÚÙºÐØ» ÞÙ» Ó¹ Ð ÓÖ ØÑ» Ó¹ Ð ÓÖ ØÑ ºÔ ½ È ØÓ Ô Ø ØÓ È Ö ÈÓ ØËÖ ÔØ ÓÖÑ Ø º Ì Ô Ô Ø Ô ÖÙÓ Ø Ä Ì ÎÁ Ú Ö ÒØ º ÌÙÖ ÒÝ ½ Å Ø Ö Ø ÓÖ Ñ ¾ ½º½ à РØ
Ë ÙÓ ÑÓ Ó ÓÑ ØÖ Ó Ð ÓÖ ØÑ ½ Ë Ú Ö Ò Ù Å ¼ Ð Ñ Ö Ø ØØÔ»»ÛÛÛºÑ ºÚÙºÐØ» ÞÙ» Ó¹ Ð ÓÖ ØÑ» Ó¹ Ð ÓÖ ØÑ ºÔ ½ È ØÓ Ô Ø ØÓ È Ö ÈÓ ØËÖ ÔØ ÓÖÑ Ø º Ì Ô Ô Ø Ô ÖÙÓ Ø Ä Ì ÎÁ Ú Ö ÒØ º ÌÙÖ ÒÝ ½ Å Ø Ö Ø ÓÖ Ñ ¾ ½º½ à РØ
 ÍÒ Ú Ö Ø Ø Ø ËØ Ú Ò Ö Å Ø ÖÓÔÔ Ú ¾¼½½ Ê ÒØ Ò Ö ÓÒº ÖÛ Ò ÝÒ Ñ Ø ÓÖ ÓÖ Ö ÓÒ ÓÑ ØÖ º Á Å Ö ÇÙ º ÒÙ Ö ¾¼½¾ ¾ Ë ÑÑ Ò Ö Ì Ñ Ø ÓÖ Ñ Ø ÖÓÔÔ Ú Ò Ö Ð Ñ ÒØ Ö ÝÒ Ñ Ø ÓÖ ÓÖ Ö ÒØ Ò ¹ Ö ÓÒ º ÇÔÔ Ú Ò Ö ÙØ Ò ÔÙÒ Ø º º
ÍÒ Ú Ö Ø Ø Ø ËØ Ú Ò Ö Å Ø ÖÓÔÔ Ú ¾¼½½ Ê ÒØ Ò Ö ÓÒº ÖÛ Ò ÝÒ Ñ Ø ÓÖ ÓÖ Ö ÓÒ ÓÑ ØÖ º Á Å Ö ÇÙ º ÒÙ Ö ¾¼½¾ ¾ Ë ÑÑ Ò Ö Ì Ñ Ø ÓÖ Ñ Ø ÖÓÔÔ Ú Ò Ö Ð Ñ ÒØ Ö ÝÒ Ñ Ø ÓÖ ÓÖ Ö ÒØ Ò ¹ Ö ÓÒ º ÇÔÔ Ú Ò Ö ÙØ Ò ÔÙÒ Ø º º
Ê ÙÐ Ö Ò Ò ÙÐ Ö ß ÐÓ Ò Ó «Ö Ò ÓÖÖ Ø ÑÙÐØ Ø Ô Ñ Ø Ó ÓÖ ÒÓÒ Ø «Ò ܹ¾ ÖÑ Ò Ö Ú ÐÓ ½ Ô ÖØÑ ÒØ Ó Ë ÒØ ÓÑÔÙØ Ò Ò ËØ Ø Ø Ë Ñ ÓÒ ÓÐ Ú Ö ÍÒ Ú Ö ØÝ Ô ÖØ Ó ¼¼¼ Ö
 ÊÙÐÖ ÙÐÖ ßÐÓ Ó «Ö ÓÖÖØ ÑÙÐØ ØÔ ÑØÓ ÓÖ Ó Ø«Ü¹¾ ÖÑ ÖÚÐÓ ½ ÔÖØÑØ Ó ËØ ÓÑÔÙØ ËØØ Ø ËÑÓ ÓÐÚÖ ÍÚÖ ØÝ ÔÖØÓ ¼¼¼ Ö ½¼¼¹ ÎÞÙÐ Ñ ÑºÙ ºÚµ ÐÙ ĐÙÖÖ Ù Ø ËĐÓÖÐ ¾ ÆÙÑÖÐ ÐÝ ØÖ ÓÖ ÅØÑØÐ Ë ÄÙ ÍÚÖ ØÝ ÓÜ ½½ ˹¾¾½ ¼¼ ÄÙ ËÛ ÐÙ
ÊÙÐÖ ÙÐÖ ßÐÓ Ó «Ö ÓÖÖØ ÑÙÐØ ØÔ ÑØÓ ÓÖ Ó Ø«Ü¹¾ ÖÑ ÖÚÐÓ ½ ÔÖØÑØ Ó ËØ ÓÑÔÙØ ËØØ Ø ËÑÓ ÓÐÚÖ ÍÚÖ ØÝ ÔÖØÓ ¼¼¼ Ö ½¼¼¹ ÎÞÙÐ Ñ ÑºÙ ºÚµ ÐÙ ĐÙÖÖ Ù Ø ËĐÓÖÐ ¾ ÆÙÑÖÐ ÐÝ ØÖ ÓÖ ÅØÑØÐ Ë ÄÙ ÍÚÖ ØÝ ÓÜ ½½ ˹¾¾½ ¼¼ ÄÙ ËÛ ÐÙ
IMM DACE A MATLAB KRIGING TOOLBOX VERSION 2.0. Søren N. Lophaven Hans Bruun Nielsen Jacob Søndergaard TECHNICAL REPORT IMM-REP
 IMM INFORMATICS AND MATHEMATICAL MODELLING Technical University of Denmark DK-2800 Kongens Lyngby Denmark J. No. DACE1 1.8.2002 HBN/ms DACE A MATLAB KRIGING TOOLBOX VERSION 2.0 Søren N. Lophaven Hans Bruun
IMM INFORMATICS AND MATHEMATICAL MODELLING Technical University of Denmark DK-2800 Kongens Lyngby Denmark J. No. DACE1 1.8.2002 HBN/ms DACE A MATLAB KRIGING TOOLBOX VERSION 2.0 Søren N. Lophaven Hans Bruun
arxiv: v1 [cond-mat.mtrl-sci] 7 May 2009
![arxiv: v1 [cond-mat.mtrl-sci] 7 May 2009 arxiv: v1 [cond-mat.mtrl-sci] 7 May 2009](/thumbs/103/161362894.jpg) ÎÖØÓÒÐ ÔÖÓÔÖØ Ó ÖÔÒ ÒÒÓÖÓÒ Ý Ö Ø¹ÔÖÒÔÐ ÐÙÐØÓÒ ÊÓÐÒ ÐÐÒ ÅÖÐ ÅÓÖ ÂÒÒ ÅÙÐØÞ Ò Ö ØÒ ÌÓÑ Ò arxiv:0905.1035v1 [cond-mat.mtrl-sci] 7 May 2009 ÁÒ ØØÙØ Ö ØÖÔÖÔÝ ÌÒ ÍÒÚÖ ØØ ÖÐÒ ÀÖÒÖ ØÖº ½¼¾ ÖÐÒ Ø ÇØÓÖ ½ ¾¼½µ ØÖØ
ÎÖØÓÒÐ ÔÖÓÔÖØ Ó ÖÔÒ ÒÒÓÖÓÒ Ý Ö Ø¹ÔÖÒÔÐ ÐÙÐØÓÒ ÊÓÐÒ ÐÐÒ ÅÖÐ ÅÓÖ ÂÒÒ ÅÙÐØÞ Ò Ö ØÒ ÌÓÑ Ò arxiv:0905.1035v1 [cond-mat.mtrl-sci] 7 May 2009 ÁÒ ØØÙØ Ö ØÖÔÖÔÝ ÌÒ ÍÒÚÖ ØØ ÖÐÒ ÀÖÒÖ ØÖº ½¼¾ ÖÐÒ Ø ÇØÓÖ ½ ¾¼½µ ØÖØ
ËØ Ø ËÐ Ò ÅÓØ ÓÒ È ÒÓÑ Ò Ò ÝÒ Ñ Ð ËÝ Ø Ñ Á ÓÖ º ÂÙÒ Ö ÂÓ Ò Âº ËØ Ð ÍÒ Ú Ö Ø Ø Ð Ð Ì Ò ÙÐØ Ø Æ ÙÖÓ Ò ÓÖÑ Ø ÍÒ Ú Ö Ø Ø ØÖ ¾ Ð Ð ½ Ê ÙÒ ÖØ ºÙÒ ¹ Ð Ð º Ø
 ËØØ ËÐÒ ÅÓØÓÒ ÈÒÓÑÒ Ò ÝÒÑÐ ËÝ ØÑ ÁÓÖ º ÂÙÒÖ ÂÓÒ Âº ËØÐ ÍÒÚÖ ØØ ÐÐ ÌÒ ÙÐØØ ÆÙÖÓÒÓÖÑØ ÍÒÚÖ ØØ ØÖ ¾ ÐÐ Ê ÙÒÖغÙÒ¹Ðк ØÐغÙÒ¹Ðк ØÖØ Ï ÔÖ ÒØ ÒÛ ØÝÔ Ó ÐÒ ÑÓØÓÒ Û Ö ÙÐØ ÖÓÑ ÒÓÚÐ Ó Ó Ø ÐÒ ÙÖ º Ï Ù Ø ØÓ Ò Ø Ù
ËØØ ËÐÒ ÅÓØÓÒ ÈÒÓÑÒ Ò ÝÒÑÐ ËÝ ØÑ ÁÓÖ º ÂÙÒÖ ÂÓÒ Âº ËØÐ ÍÒÚÖ ØØ ÐÐ ÌÒ ÙÐØØ ÆÙÖÓÒÓÖÑØ ÍÒÚÖ ØØ ØÖ ¾ ÐÐ Ê ÙÒÖغÙÒ¹Ðк ØÐغÙÒ¹Ðк ØÖØ Ï ÔÖ ÒØ ÒÛ ØÝÔ Ó ÐÒ ÑÓØÓÒ Û Ö ÙÐØ ÖÓÑ ÒÓÚÐ Ó Ó Ø ÐÒ ÙÖ º Ï Ù Ø ØÓ Ò Ø Ù
Instituto de Sistemas e Robótica. Pólo de Lisboa
 ÄÖÒÒ ÚÓÖ¹ ÐØÓÒ Ò ÑÙÐعÓÐ ÖÓÓØ Ø ËÒÖ ÐÖ ÒÓ ÄÙ Ù ØÓÓ Ê̹¼½¹¼¾ Instituto de Sistemas e Robótica Pólo de Lisboa ÄÖÒÒ ÚÓÖ¹ ÐØÓÒ Ò ÑÙÐعÓÐ ÖÓÓØ Ø ËÒÖ ÐÖ ÒÓ ÖÙÖÝ ¾¼¼¾ Ê̹¼½¹¼¾ ÄÙ Ù ØÓÓ ÁËÊ ÌÓÖÖ ÆÓÖØ Úº ÊÓÚ Ó
ÄÖÒÒ ÚÓÖ¹ ÐØÓÒ Ò ÑÙÐعÓÐ ÖÓÓØ Ø ËÒÖ ÐÖ ÒÓ ÄÙ Ù ØÓÓ Ê̹¼½¹¼¾ Instituto de Sistemas e Robótica Pólo de Lisboa ÄÖÒÒ ÚÓÖ¹ ÐØÓÒ Ò ÑÙÐعÓÐ ÖÓÓØ Ø ËÒÖ ÐÖ ÒÓ ÖÙÖÝ ¾¼¼¾ Ê̹¼½¹¼¾ ÄÙ Ù ØÓÓ ÁËÊ ÌÓÖÖ ÆÓÖØ Úº ÊÓÚ Ó
ÈÖÓ Ò ÙÖÓÈÎÅ»ÅÈÁ ¾¼¼ Ë Ôº ½ ¹¾¾ Ù Ô Ø ÀÙÒ ÖÝ ÄÆ Ë ËÔÖ Ò Ö¹Î ÖÐ ¾¼¼ º ËÔÖ Ò Ö¹Î ÖÐ ØØÔ»»ÛÛÛº ÔÖ Ò Öº»ÓÑÔ»ÐÒ» Ò Üº ØÑÐ ÅÓÖ Æ ÒØ Ê ÙØ ÓÒ Ð ÓÖ Ø Ñ ÓÖ ÆÓÒ¹
 ÈÖÓÒ ÙÖÓÈÎÅ»ÅÈÁ ¾¼¼ ËÔº ½¹¾¾ ÙÔ Ø ÀÙÒÖÝ ÄÆË ËÔÖÒÖ¹ÎÖÐ ¾¼¼º ËÔÖÒÖ¹ÎÖÐ ØØÔ»»ÛÛÛº ÔÖÒÖº»ÓÑÔ»ÐÒ»ÒܺØÑÐ ÅÓÖ ÆÒØ ÊÙØÓÒ ÐÓÖØÑ ÓÖ ÆÓÒ¹ÔÓÛÖ¹Ó¹ØÛÓ ÆÙÑÖ Ó ÈÖÓ ÓÖ Ò Å ¹È Ò ÈÖÐÐÐ ËÝ ØÑ ÊÓÐ ÊÒ ÒÖ ½ Ò Â ÔÖ ÄÖ ÓÒ ÌÖĐ«¾
ÈÖÓÒ ÙÖÓÈÎÅ»ÅÈÁ ¾¼¼ ËÔº ½¹¾¾ ÙÔ Ø ÀÙÒÖÝ ÄÆË ËÔÖÒÖ¹ÎÖÐ ¾¼¼º ËÔÖÒÖ¹ÎÖÐ ØØÔ»»ÛÛÛº ÔÖÒÖº»ÓÑÔ»ÐÒ»ÒܺØÑÐ ÅÓÖ ÆÒØ ÊÙØÓÒ ÐÓÖØÑ ÓÖ ÆÓÒ¹ÔÓÛÖ¹Ó¹ØÛÓ ÆÙÑÖ Ó ÈÖÓ ÓÖ Ò Å ¹È Ò ÈÖÐÐÐ ËÝ ØÑ ÊÓÐ ÊÒ ÒÖ ½ Ò Â ÔÖ ÄÖ ÓÒ ÌÖĐ«¾
Ð ÓÖ Ø Ñ ÓÖ ÌÖ Ò ÔÓ Ø ÓÒ ÁÒÚ Ö ÒØ ËØÖ Ò Å Ø Ò ÜØ Ò ØÖ Øµ Î Ð Å Ò Ò ½ ÓÒÞ ÐÓ Æ Ú ÖÖÓ ¾ Ò Ó Í ÓÒ Ò ½ ¾ ½ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÈºÇ ÓÜ ¾ Ì ÓÐÐ ÙÙ ØÙ ¾ µ
 ÐÓÖØÑ ÓÖ ÌÖÒ ÔÓ ØÓÒ ÁÒÚÖÒØ ËØÖÒ ÅØÒ ÜØÒ ØÖص ÎÐ ÅÒÒ ½ ÓÒÞÐÓ ÆÚÖÖÓ ¾ Ò Ó ÍÓÒÒ ½ ¾ ½ ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ ÈºÇ ÓÜ ¾ ÌÓÐÐ ÙÙ ØÙ ¾ µ Áƹ¼¼¼½ ÍÒÚÖ ØÝ Ó ÀÐ Ò ÒÐÒº ßÚÑÒÒ ÙÓÒÒÐ ºÐ Òº ÒØÖ ÓÖ Ï Ê Ö ÔÖØÑÒØ Ó ÓÑÔÙØÖ
ÐÓÖØÑ ÓÖ ÌÖÒ ÔÓ ØÓÒ ÁÒÚÖÒØ ËØÖÒ ÅØÒ ÜØÒ ØÖص ÎÐ ÅÒÒ ½ ÓÒÞÐÓ ÆÚÖÖÓ ¾ Ò Ó ÍÓÒÒ ½ ¾ ½ ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ ÈºÇ ÓÜ ¾ ÌÓÐÐ ÙÙ ØÙ ¾ µ Áƹ¼¼¼½ ÍÒÚÖ ØÝ Ó ÀÐ Ò ÒÐÒº ßÚÑÒÒ ÙÓÒÒÐ ºÐ Òº ÒØÖ ÓÖ Ï Ê Ö ÔÖØÑÒØ Ó ÓÑÔÙØÖ
 ÅØÑØ Ò ØØÙØØ ÖÐ Ö ÚÐÒÒÖ ÓÑ ØÖÑÒÒØÖ Ú ÙÒØÙØÓÑÓÖÖ ÀÒ ÂÖÒ ÊÖÚÓÐ ÀÓÚÓÔÔÚ ÑØÑØ ÎÖÒ ¾¼¼¾ ÓÖÓÖ À ØÓÖÒ ÒÒ ÓÔÔÚÒ Ö Ø ÔÖ Ö ØÐ Ó Ö ØØ ÙØ ÔÖÒ Ö ÄÛ Ó ÆÐ ÚÖÐ ÖÖ ÓÑÔÐ ÒÐÝ º ÖÖØ ÒÑÐ Ñ ÑÒ ÚÐÖ ÓÑ ØØÖ ÚÖØ Ò ÑÙÐ ÓÚÓÔÔÚ ÔÖÓÐÑغ
ÅØÑØ Ò ØØÙØØ ÖÐ Ö ÚÐÒÒÖ ÓÑ ØÖÑÒÒØÖ Ú ÙÒØÙØÓÑÓÖÖ ÀÒ ÂÖÒ ÊÖÚÓÐ ÀÓÚÓÔÔÚ ÑØÑØ ÎÖÒ ¾¼¼¾ ÓÖÓÖ À ØÓÖÒ ÒÒ ÓÔÔÚÒ Ö Ø ÔÖ Ö ØÐ Ó Ö ØØ ÙØ ÔÖÒ Ö ÄÛ Ó ÆÐ ÚÖÐ ÖÖ ÓÑÔÐ ÒÐÝ º ÖÖØ ÒÑÐ Ñ ÑÒ ÚÐÖ ÓÑ ØØÖ ÚÖØ Ò ÑÙÐ ÓÚÓÔÔÚ ÔÖÓÐÑغ
ÍÌ Ù Ø Ò Î ÐÐ ¾¼¼ Æ Û ÊÓ Ó ÙÔ ÓÙÖ¹Ä Ì Ñ È Ø Ö ËØÓÒ ÃÙÖØ Ö Ò Ö Ë Ð Ñ Ìº Ö Ó Ò È Ý ÐÑ Ò Æ ÓРú ÂÓÒ Æ Ø ÃÓ Ð Ö ÓÖÝ ÃÙ ÐÑ ÒÒ ÐÐ Ä Ò ÅÓ Ò ËÖ Ö Ò Ò Ð ËØÖÓÒ
 ÍÌ Ù ØÒ ÎÐÐ ¾¼¼ ÆÛ ÊÓÓÙÔ ÓÙÖ¹Ä ÌÑ ÈØÖ ËØÓÒ ÃÙÖØ Ö ÒÖ ËÐÑ Ìº ÖÓÒ ÈÝ ÐÑÒ ÆÓРú ÂÓÒ ÆØ ÃÓÐ ÖÓÖÝ ÃÙÐÑÒÒ ÐÐ ÄÒ ÅÓÒ ËÖÖÒ ÒÐ ËØÖÓÒÖ ÙÖÙ ÝÑ ÀÖÖÒ ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ Ì ÍÒÚÖ ØÝ Ó ÌÜ Ø Ù ØÒ ½ ÍÒÚÖ ØÝ ËØØÓÒ ¼¼¼ Ù
ÍÌ Ù ØÒ ÎÐÐ ¾¼¼ ÆÛ ÊÓÓÙÔ ÓÙÖ¹Ä ÌÑ ÈØÖ ËØÓÒ ÃÙÖØ Ö ÒÖ ËÐÑ Ìº ÖÓÒ ÈÝ ÐÑÒ ÆÓРú ÂÓÒ ÆØ ÃÓÐ ÖÓÖÝ ÃÙÐÑÒÒ ÐÐ ÄÒ ÅÓÒ ËÖÖÒ ÒÐ ËØÖÓÒÖ ÙÖÙ ÝÑ ÀÖÖÒ ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ Ì ÍÒÚÖ ØÝ Ó ÌÜ Ø Ù ØÒ ½ ÍÒÚÖ ØÝ ËØØÓÒ ¼¼¼ Ù
arxiv:math.dg/ v1 15 Nov 2004
 arxiv:math.dg/0411334 v1 15 Nov 2004 ÇÒ Ø ÃË ÈÖÒ ÓÖ ÃĐÐÖ ÉÙÒØÞØÓÒ Ó Ø ÓØÒÒØ ÙÒÐ Ó Ä ÖÓÙÔ ÖÐÓ ÐÓÖÒØÒÓ Ý ÈÖÓ ÅØ Þ ÂÓ ÅÓÙÖÓ Ý Ò ÂÓÓ Èº ÆÙÒ Ý ÅÖ ¼¼ ØÖØ ÒØÙÖÐ ÓÒ¹ÔÖÑØÖ ÑÐÝ Ó ÃĐÐÖ ÕÙÒØÞØÓÒ Ó Ø ÓØÒÒØ ÙÒÐ Ó ÓÑÔØ
arxiv:math.dg/0411334 v1 15 Nov 2004 ÇÒ Ø ÃË ÈÖÒ ÓÖ ÃĐÐÖ ÉÙÒØÞØÓÒ Ó Ø ÓØÒÒØ ÙÒÐ Ó Ä ÖÓÙÔ ÖÐÓ ÐÓÖÒØÒÓ Ý ÈÖÓ ÅØ Þ ÂÓ ÅÓÙÖÓ Ý Ò ÂÓÓ Èº ÆÙÒ Ý ÅÖ ¼¼ ØÖØ ÒØÙÖÐ ÓÒ¹ÔÖÑØÖ ÑÐÝ Ó ÃĐÐÖ ÕÙÒØÞØÓÒ Ó Ø ÓØÒÒØ ÙÒÐ Ó ÓÑÔØ
NORGES TEKNISK- NATURVITENSKAPELIGE UNIVERSITET INSTITUTT FOR KJEMI
 NORGES EKNISK- NAURIENSKAPELIGE UNIERSIE INSIU FOR KJEMI KJ4160 FYSIKALSK KJEMI GK, ÅREN 2008 Onsdag 28. mai 2008 id: 9.00-13.00 Faglig kontakt under eksamen: Førsteaman. Morten Bjørgen, tlf. 47 28 88
NORGES EKNISK- NAURIENSKAPELIGE UNIERSIE INSIU FOR KJEMI KJ4160 FYSIKALSK KJEMI GK, ÅREN 2008 Onsdag 28. mai 2008 id: 9.00-13.00 Faglig kontakt under eksamen: Førsteaman. Morten Bjørgen, tlf. 47 28 88
En ekte involusjon på Waldhausens rigid-tube - avbildning. Sverre An dré Lun øe-n ielsen. Skriftlig del av Cand. Scient. -graden i matematikk
 Universitetet i O slo M atematisk I nstitutt En ekte involusjon på Waldhausens rigid-tube - avbildning Sverre An dré Lun øe-n ielsen Skriftlig del av Cand. Scient. -graden i matematikk 2. mai 2000 ÁÒÒÓÐ
Universitetet i O slo M atematisk I nstitutt En ekte involusjon på Waldhausens rigid-tube - avbildning Sverre An dré Lun øe-n ielsen Skriftlig del av Cand. Scient. -graden i matematikk 2. mai 2000 ÁÒÒÓÐ
PDF created with pdffactory Pro trial version
 [ ² Ú»» ³»»² ¾ ²» ¹» ô Ì ± « Forord Ò ; ±¹ ²» ³«¹»» òòò [ ²»² ª ; µ«² ¹» ¼» º± îðïéô ¹ «²²»² ¼»»» ¼» µ±³³» ² ³³» ² º± ¾ ²» ¹» «¹«±³ ¹ ( ¼» ¾»²¼ ²¹»»²»» ; ²» ò Ê»² : ¼»» ª µ ¹ ±¾¾ ±¹ ¼»² µ ª º± ª» ¹±¼ ò
[ ² Ú»» ³»»² ¾ ²» ¹» ô Ì ± « Forord Ò ; ±¹ ²» ³«¹»» òòò [ ²»² ª ; µ«² ¹» ¼» º± îðïéô ¹ «²²»² ¼»»» ¼» µ±³³» ² ³³» ² º± ¾ ²» ¹» «¹«±³ ¹ ( ¼» ¾»²¼ ²¹»»²»» ; ²» ò Ê»² : ¼»» ª µ ¹ ±¾¾ ±¹ ¼»² µ ª º± ª» ¹±¼ ò
½ ÔÔÐ Ø ÓÒ Ó Ê ÓÒ ÙÖ Ð ÇÊ Á Ö Ø ØÙÖ Ç Ö Å Ò Ö ÄÙ Ë Ñ Ö Å ÖØ Ò ÅÓÖ Â Ò¹Å Ö ÐÓ Ñ ØÖ Ø Ê ÓÒ ÙÖ Ø ÓÒ Ò Ð Ø ÔØ ÓÒ Ó ÓÓÖ Ò Ø ÊÓØ Ø ÓÒ Á Ø Ð ÓÑÔÙØ Ö ÇÊ Á µ Ù
 ½ ÔÔÐØÓÒ Ó ÊÓÒ ÙÖÐ ÇÊÁ ÖØØÙÖ Ç Ö ÅÒÖ ÄÙ ËÑÖ ÅÖØÒ ÅÓÖ ÂÒ¹ÅÖ ÐÓ Ñ ØÖØ ÊÓÒ ÙÖØÓÒ ÒÐ Ø ÔØÓÒ Ó ÓÓÖÒØ ÊÓØØÓÒ ÁØÐ ÓÑÔÙØÖ ÇÊÁµ ÙÒØ ØÓ Ø Ô Ò Ó Ø Ó ÔÔй ØÓÒ Ò ÖØÒ ÔÔÐØÓÒ Ô ÇÊÁ¹ ØÝÐ ÑÔÐÑÒØØÓÒ º ÊÓÒ ÙÖØÓÒ Ò ÑÔÐÑÒØ
½ ÔÔÐØÓÒ Ó ÊÓÒ ÙÖÐ ÇÊÁ ÖØØÙÖ Ç Ö ÅÒÖ ÄÙ ËÑÖ ÅÖØÒ ÅÓÖ ÂÒ¹ÅÖ ÐÓ Ñ ØÖØ ÊÓÒ ÙÖØÓÒ ÒÐ Ø ÔØÓÒ Ó ÓÓÖÒØ ÊÓØØÓÒ ÁØÐ ÓÑÔÙØÖ ÇÊÁµ ÙÒØ ØÓ Ø Ô Ò Ó Ø Ó ÔÔй ØÓÒ Ò ÖØÒ ÔÔÐØÓÒ Ô ÇÊÁ¹ ØÝÐ ÑÔÐÑÒØØÓÒ º ÊÓÒ ÙÖØÓÒ Ò ÑÔÐÑÒØ
Ò Ë ÙÐ Ò È Ö ÓÖÑ Ò Ò Ø ÓÖ Ò ¹ Ö Ò ËÝÒ ÖÓÒ Þ Ø ÓÒ ÖÓÖ º Ø Ð ÓÒ Ä ÖÖÝ ÊÙ ÓÐÔ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Ì À Ö Û ÍÒ Ú Ö ØÝ Ó Â ÖÙ Ð Ñ ½ ¼ Â ÖÙ Ð Ñ Á Ö Ð ØÖ Ø
 Ò ËÙÐÒ ÈÖÓÖÑÒ Ò Ø ÓÖ Ò¹ÖÒ ËÝÒÖÓÒÞØÓÒ ÖÓÖ º ØÐ ÓÒ ÄÖÖÝ ÊÙÓÐÔ ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ Ì ÀÖÛ ÍÒÚÖ ØÝ Ó ÂÖÙ ÐÑ ½¼ ÂÖÙ ÐÑ Á ÖÐ ØÖØ ÅÙÐØÔÖÓÖÑÑ ÑÙÐØÔÖÓ ÓÖ ÜÙØÒ Ò¹ÖÒ ÔÖÐÐÐ ÔÖÓÖÑ ÔÔÖ ØÓ ÖÕÙÖ ÒÛ ÙÐÒ ÔÓÐ º ÔÖÓÑ Ò ÒÛ Ò
Ò ËÙÐÒ ÈÖÓÖÑÒ Ò Ø ÓÖ Ò¹ÖÒ ËÝÒÖÓÒÞØÓÒ ÖÓÖ º ØÐ ÓÒ ÄÖÖÝ ÊÙÓÐÔ ÔÖØÑÒØ Ó ÓÑÔÙØÖ ËÒ Ì ÀÖÛ ÍÒÚÖ ØÝ Ó ÂÖÙ ÐÑ ½¼ ÂÖÙ ÐÑ Á ÖÐ ØÖØ ÅÙÐØÔÖÓÖÑÑ ÑÙÐØÔÖÓ ÓÖ ÜÙØÒ Ò¹ÖÒ ÔÖÐÐÐ ÔÖÓÖÑ ÔÔÖ ØÓ ÖÕÙÖ ÒÛ ÙÐÒ ÔÓÐ º ÔÖÓÑ Ò ÒÛ Ò
ÓÒØÒØ ½ ÖÙÒÒÐÒ ÖÔÖº ¾ ÔÖÑØÚØ ÖÙÖ Ú ÙÒ ÓÒÒ ÖÞÓÖÞÝÖÖØ ½ Æ ØØ ÖÙÖ ÓÒº ¾ ÃÐÑÖÐÑÒØÖ ÙÒ ÓÒÒ ¾ ÖÙÖ Ú ÙÒ ÓÒÒ ÅÒÖ ¾ ¹ÖÙÖ Ú ÙÒ ÓÒÒ ½
 ÀǹÒÓØØ ¾¼¼¼ ÒÖ ¾ ÁËÆ ¾¹¹¼½¹ ÁËËÆ ¼¼¹½¼ ÄØØ ÙÖÙÖ ÓÒ ØÓÖ Ó Ò ÑÒÖ ÖÙÖ ÓÒ ØÓÖ ÄÖ ÃÖ ØÒ Ò ¹ÑÐ ÐÖ ÖÙºÓ ÐÓºÒÓ ÃÓÑÔÒÙÑ À ÓÐÒ Ç ÐÓ ÚÐÒ ÓÖ ÒÒÖÙØÒÒÒ ¾¼¼¼ ÓÒØÒØ ½ ÖÙÒÒÐÒ ÖÔÖº ¾ ÔÖÑØÚØ ÖÙÖ Ú ÙÒ ÓÒÒ ÖÞÓÖÞÝÖÖØ ½ Æ ØØ
ÀǹÒÓØØ ¾¼¼¼ ÒÖ ¾ ÁËÆ ¾¹¹¼½¹ ÁËËÆ ¼¼¹½¼ ÄØØ ÙÖÙÖ ÓÒ ØÓÖ Ó Ò ÑÒÖ ÖÙÖ ÓÒ ØÓÖ ÄÖ ÃÖ ØÒ Ò ¹ÑÐ ÐÖ ÖÙºÓ ÐÓºÒÓ ÃÓÑÔÒÙÑ À ÓÐÒ Ç ÐÓ ÚÐÒ ÓÖ ÒÒÖÙØÒÒÒ ¾¼¼¼ ÓÒØÒØ ½ ÖÙÒÒÐÒ ÖÔÖº ¾ ÔÖÑØÚØ ÖÙÖ Ú ÙÒ ÓÒÒ ÖÞÓÖÞÝÖÖØ ½ Æ ØØ
Recorded signals in time. Transducers Array. Recorded signals in time. Transducers Array
 ÌÁÅ ÊÎÊËÄ Æ ÊÇÍËÁÆ ÁÆ ÊÆÇÅ ÅÁ ÍÁÄÄÍÅ Ä Æ ÄÇÆÁ ÊÀÁÃ Ý ØÖغ ÁÒ ØÑ ÖÚÖ Ð ÓÙ Ø ÜÔÖÑÒØ ÒÐ ÑØØ ÖÓÑ ÐÓÐÞ ÓÙÖ ÖÓÖ Ø Ò ÖÖÝ Ó ÖÚÖ ØÑ ÖÚÖ Ò ÒÐÐÝ Ö¹ÑØØ ÒØÓ Ø ÑÙѺ ÐÖØ ØÙÖ Ó ØÑ ÖÚÖ Ð ÜÔÖÑÒØ ØØ Ø ÖÓÙ Ò Ó Ø Ö¹ÑØØ ÒÐ
ÌÁÅ ÊÎÊËÄ Æ ÊÇÍËÁÆ ÁÆ ÊÆÇÅ ÅÁ ÍÁÄÄÍÅ Ä Æ ÄÇÆÁ ÊÀÁÃ Ý ØÖغ ÁÒ ØÑ ÖÚÖ Ð ÓÙ Ø ÜÔÖÑÒØ ÒÐ ÑØØ ÖÓÑ ÐÓÐÞ ÓÙÖ ÖÓÖ Ø Ò ÖÖÝ Ó ÖÚÖ ØÑ ÖÚÖ Ò ÒÐÐÝ Ö¹ÑØØ ÒØÓ Ø ÑÙѺ ÐÖØ ØÙÖ Ó ØÑ ÖÚÖ Ð ÜÔÖÑÒØ ØØ Ø ÖÓÙ Ò Ó Ø Ö¹ÑØØ ÒÐ
Թػ¼½¼ ¼ ÍÏÌ È ¹¾¼¼½¹½ ÌÍϹ¼½¹¼½¾ Ê ÒÓÖÑ Ð Þ Ø ÓÒ Ó Ø ÒÓÒÓÑÑÙØ Ø Ú Ô ÓØÓÒ Ð ¹ Ò Ö Ý ØÓ ÐÐ ÓÖ Ö Ú Ë Ö ¹Ï ØØ Ò Ñ Ô Ò Ö Ð ½ Â Ô Ö Ö Ñ ØÖÙÔ ¾ À Ö Ð ÖÓ ÄÙ
 Թػ¼¼¼ ÍÏÌȹ¼¼¹ ÌÍϹ¼¹¼ ÊÒÓÖÑÞØÓÒ Ó Ø ÒÓÒÓÑÑÙØØÚ ÔÓØÓÒ ¹ÒÖÝ ØÓ ÓÖÖ Ú ËÖ¹ÏØØÒ ÑÔ ÒÖ Â ÔÖ ÖÑ ØÖÙÔ ÀÖ ÖÓ ÄÙ ÈÓÔÔ ÅÒÖ ËÛ ÊÑÖ ÏÙÒÖ ÁÒ ØØÙØ ĐÙÖ ÌÓÖØ ÈÝ ÌÒ ÍÒÚÖ ØĐØ ÏÒ ÏÒÖ ÀÙÔØ ØÖ ¹¼ ¹¼¼ ÏÒ Ù ØÖ ÁÒ ØØÙØ ĐÙÖ
Թػ¼¼¼ ÍÏÌȹ¼¼¹ ÌÍϹ¼¹¼ ÊÒÓÖÑÞØÓÒ Ó Ø ÒÓÒÓÑÑÙØØÚ ÔÓØÓÒ ¹ÒÖÝ ØÓ ÓÖÖ Ú ËÖ¹ÏØØÒ ÑÔ ÒÖ Â ÔÖ ÖÑ ØÖÙÔ ÀÖ ÖÓ ÄÙ ÈÓÔÔ ÅÒÖ ËÛ ÊÑÖ ÏÙÒÖ ÁÒ ØØÙØ ĐÙÖ ÌÓÖØ ÈÝ ÌÒ ÍÒÚÖ ØĐØ ÏÒ ÏÒÖ ÀÙÔØ ØÖ ¹¼ ¹¼¼ ÏÒ Ù ØÖ ÁÒ ØØÙØ ĐÙÖ
compute node I/O node compute node compute node interconnection network I/O node compute node compute node I/O node compute node I/O node compute node
 Ì Î Ø ÈÖÐÐÐ Ð ËÝ ØÑ ÈØÖ ÓÖØØ ÖÓÖ ØÐ ÓÒ ÁÅ Ì Â ÏØ ÓÒ Ê Ö ÒØÖ È Ç ÓÜ ¾½ ÓÖØÓÛÒ ÀØ Æ ½¼ ÂÙÐÝ ¾¼¼½ ØÖØ Ì Î Ø ÔÖÐÐÐ Ð Ý ØÑ Ò ØÓ ÔÖÓÚ ÔÖÐÐÐ Ð ØÓ ÔÔÐØÓÒ ÔÖÓÖÑ ÖÙÒÒÒ ÓÒ ÑÙÐØÓÑÔÙØÖ ÛØ ÔÖÐÐÐ Á»Ç Ù Ý ØÑ Î Ø Ù ÒÛ
Ì Î Ø ÈÖÐÐÐ Ð ËÝ ØÑ ÈØÖ ÓÖØØ ÖÓÖ ØÐ ÓÒ ÁÅ Ì Â ÏØ ÓÒ Ê Ö ÒØÖ È Ç ÓÜ ¾½ ÓÖØÓÛÒ ÀØ Æ ½¼ ÂÙÐÝ ¾¼¼½ ØÖØ Ì Î Ø ÔÖÐÐÐ Ð Ý ØÑ Ò ØÓ ÔÖÓÚ ÔÖÐÐÐ Ð ØÓ ÔÔÐØÓÒ ÔÖÓÖÑ ÖÙÒÒÒ ÓÒ ÑÙÐØÓÑÔÙØÖ ÛØ ÔÖÐÐÐ Á»Ç Ù Ý ØÑ Î Ø Ù ÒÛ
ÁÒ ÓÖÑ Ø ÓÒ ÐÓÛ ÁÒ Ö Ò ÓÖ ÅÄ Ö Ò Ó ÈÓØØ Ö Ö ÒÓ ºÈÓØØ Ö ÒÖ º Ö Î Ò ÒØ Ë ÑÓÒ Ø Î Ò ÒØºË ÑÓÒ Ø ÒÖ º Ö ØÖ Ø Ì Ô Ô Ö ÔÖ ÒØ ØÝÔ ¹ Ò ÓÖÑ Ø ÓÒ ÓÛ Ò ÐÝ ÓÖ Ðй
 ÁÒÓÖÑØÓÒ ÐÓÛ ÁÒÖÒ ÓÖ ÅÄ ÖÒÓ ÈÓØØÖ ÖÒÓ ºÈÓØØÖÒÖºÖ ÎÒÒØ ËÑÓÒØ ÎÒÒغËÑÓÒØÒÖºÖ ØÖØ Ì ÔÔÖ ÔÖ ÒØ ØÝÔ¹ ÒÓÖÑØÓÒ ÓÛ ÒÐÝ ÓÖ ÐйݹÚÐÙ ¹ÐÙÐÙ ÕÙÔÔ ÛØ ÖÖÒ Ü¹ ÔØÓÒ Ò ÐعÔÓÐÝÑÓÖÔ Ñ Û Û ÖÖ ØÓ ÓÖ Åĺ Ì ØÝÔ Ý ØÑ ÓÒ ØÖÒع
ÁÒÓÖÑØÓÒ ÐÓÛ ÁÒÖÒ ÓÖ ÅÄ ÖÒÓ ÈÓØØÖ ÖÒÓ ºÈÓØØÖÒÖºÖ ÎÒÒØ ËÑÓÒØ ÎÒÒغËÑÓÒØÒÖºÖ ØÖØ Ì ÔÔÖ ÔÖ ÒØ ØÝÔ¹ ÒÓÖÑØÓÒ ÓÛ ÒÐÝ ÓÖ ÐйݹÚÐÙ ¹ÐÙÐÙ ÕÙÔÔ ÛØ ÖÖÒ Ü¹ ÔØÓÒ Ò ÐعÔÓÐÝÑÓÖÔ Ñ Û Û ÖÖ ØÓ ÓÖ Åĺ Ì ØÝÔ Ý ØÑ ÓÒ ØÖÒع
PDF created with pdffactory Pro trial version
 [ ² Ú»» ³»»² ¾ ²» ¹» ô λ¹²¾² Forord Ü»²²» ²»² ¹» ¼» º ²«¼»»³¾» îðïéò a» ª ¼»»» ô ª ¼» ¾»² ² ³³» ² º± ¾ ²» ¹»²ò Ü»²²» µ ª ¾ «µ» ¼ ¾ ¹±¼ µ»² ³»¼ô ±¹ îðïè ª ²² ± ¼» ¼»²²» ªb» ³»¼»¹» ²»² ª ò»»³¾» îðïê ¼¼»
[ ² Ú»» ³»»² ¾ ²» ¹» ô λ¹²¾² Forord Ü»²²» ²»² ¹» ¼» º ²«¼»»³¾» îðïéò a» ª ¼»»» ô ª ¼» ¾»² ² ³³» ² º± ¾ ²» ¹»²ò Ü»²²» µ ª ¾ «µ» ¼ ¾ ¹±¼ µ»² ³»¼ô ±¹ îðïè ª ²² ± ¼» ¼»²²» ªb» ³»¼»¹» ²»² ª ò»»³¾» îðïê ¼¼»
PDF created with pdffactory Pro trial version
 [ ² Ú»» ³»»² ¾ ²» ¹» ô ß«¹»²¼ ¼»² Forord Ÿ ² îðïé ¹»² ¾» µ ª»» ª ¾ ²» ¹»² ±»ô»»² ±² ª ¾ ²» ¹»²ô µ µ» ± ² ²¹» ±¹ ª»¼ ¹±¹ µ» ¾» ¼ò Ð ² ¾» ¼» ¾ ²» ¹»²» ¾ ¹¹» ± ºa ¹»²¼» ³»æ ó Î ³³» ² º± ¾ ²» ¹»² ²² ± ¼ ±¹
[ ² Ú»» ³»»² ¾ ²» ¹» ô ß«¹»²¼ ¼»² Forord Ÿ ² îðïé ¹»² ¾» µ ª»» ª ¾ ²» ¹»² ±»ô»»² ±² ª ¾ ²» ¹»²ô µ µ» ± ² ²¹» ±¹ ª»¼ ¹±¹ µ» ¾» ¼ò Ð ² ¾» ¼» ¾ ²» ¹»²» ¾ ¹¹» ± ºa ¹»²¼» ³»æ ó Î ³³» ² º± ¾ ²» ¹»² ²² ± ¼ ±¹
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ Ÿ Œ œ ˆ ˆ Š Œ. .. ³μ. μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö Œ Œ ˆˆ 79 ˆ Š ˆ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 01.. 4.. 1 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ ˆƒƒ Œˆ Œ Š.. ³μ μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö ˆ 70 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ 7 ˆ ˆ IFW- ˆˆ ˆ Œ Œ Œ ˆˆ 79 Š ˆ 80 ˆ Š ˆ 81 E-mail: neznamov@vniief.ru
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 01.. 4.. 1 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ ˆƒƒ Œˆ Œ Š.. ³μ μ ± Ë ²Ó Ò Ö Ò Í É Å ˆˆ Ô± ³ É ²Ó μ Ë ±, μ, μ Ö ˆ 70 Ÿ Œ œ ˆ ˆ Š Œ ˆˆ ˆÄ 7 ˆ ˆ IFW- ˆˆ ˆ Œ Œ Œ ˆˆ 79 Š ˆ 80 ˆ Š ˆ 81 E-mail: neznamov@vniief.ru
Šˆ Ÿ Š Œ ˆˆ Ÿ ˆ Š ˆ Ÿ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2018.. 49.. 2.. 476Ä581 Œ ƒ ˆŠ Šˆ Ÿ Š Œ ˆˆ Ÿ ˆ Š ˆ Ÿ.. ƒê μ 1, 2,.. Êϱ 2,. ƒ. Ê±μ ± 1,,.. ÒÏ 2 1 Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê 2 Í μ ²Ó Ò ² μ É ²Ó ± Ö Ò Ê É É Œˆ ˆ, Œμ ± ˆ 477 Œ ˆŸ Š ˆ Šˆ Š 480
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2018.. 49.. 2.. 476Ä581 Œ ƒ ˆŠ Šˆ Ÿ Š Œ ˆˆ Ÿ ˆ Š ˆ Ÿ.. ƒê μ 1, 2,.. Êϱ 2,. ƒ. Ê±μ ± 1,,.. ÒÏ 2 1 Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê 2 Í μ ²Ó Ò ² μ É ²Ó ± Ö Ò Ê É É Œˆ ˆ, Œμ ± ˆ 477 Œ ˆŸ Š ˆ Šˆ Š 480
ก ก. ก.. Website : ก ก ก ก ก
 ก ก ก.. Website : Http://province.m-culture.go.th/kamphangphet ก ก ก ก ก å a å a a a å a a ก ก ก. ก ก ก ก ก ก ก ก ก... ก oe i e и å ae и a-e e a å þ2þ5þ5þ3 ie å и å å o åe oe o åæ e a å a и þ2þ7 u å a
ก ก ก.. Website : Http://province.m-culture.go.th/kamphangphet ก ก ก ก ก å a å a a a å a a ก ก ก. ก ก ก ก ก ก ก ก ก... ก oe i e и å ae и a-e e a å þ2þ5þ5þ3 ie å и å å o åe oe o åæ e a å a и þ2þ7 u å a
(a 1, a 2, a 3, a 4 ) ³Æ s 10. a 1 a 2 a 3 a 4 a 1 a 2 a 3 a 4. ( a 1 a 2 a 3 a 4 a 1 a 2 a 3 a 4) (a 1 a 2 a 3 a 4 a 1 a 2 a 3 a 4)
 5 à ¹¾½ 5.1 ÇÉ» Â Â Þ Kripke Ù M =< S,, I, L > ½ Đ ÞÒ S «É S 2 n Ä ĐÞ n Ê Æ Å n = 4 ÄÝ s 0, s 1, s 2,... (a 1, a 2, a 3, a 4 ) ³Æ s 10 ȹÌĐÞ ÁÆ Ü Đ ³¹Á Ü Ô Ô Ü Ä Ü Á Æ ÔÆ ¹ Ä¹Ì Å Á a 1 a 2 a 3 a 4 Æ s
5 à ¹¾½ 5.1 ÇÉ» Â Â Þ Kripke Ù M =< S,, I, L > ½ Đ ÞÒ S «É S 2 n Ä ĐÞ n Ê Æ Å n = 4 ÄÝ s 0, s 1, s 2,... (a 1, a 2, a 3, a 4 ) ³Æ s 10 ȹÌĐÞ ÁÆ Ü Đ ³¹Á Ü Ô Ô Ü Ä Ü Á Æ ÔÆ ¹ Ä¹Ì Å Á a 1 a 2 a 3 a 4 Æ s
P ±Ê. Š - ˆ Œˆ œ Ÿ Š ˆŒ ˆŸ ƒ Ÿ Š Œ ˆ ŠˆŒ. ² μ Ê ² Œ É ³ É Î ±μ ³μ ² μ.
 P-22-86.. ±Ê Š - ˆŒˆ œÿ Š ˆŒ ˆŸ ƒ Ÿ Š Œ ˆ ŠˆŒ ˆ Œ ² μ Ê ² Œ É ³ É Î ±μ ³μ ² μ E-mail: dnd@jinr.ru ±Ê.. P-22-86 ŠÊ μî μ- μ² μ³ ²Ó Ö μ± ³ Í Ö Ï Éμ μ μ Ö ± Éμ³ É Î ± ³ μ Ê ³ Ê ²μ ŠμÔËË Í ÉÒ ³μ ² ²μ± ²Ó μ
P-22-86.. ±Ê Š - ˆŒˆ œÿ Š ˆŒ ˆŸ ƒ Ÿ Š Œ ˆ ŠˆŒ ˆ Œ ² μ Ê ² Œ É ³ É Î ±μ ³μ ² μ E-mail: dnd@jinr.ru ±Ê.. P-22-86 ŠÊ μî μ- μ² μ³ ²Ó Ö μ± ³ Í Ö Ï Éμ μ μ Ö ± Éμ³ É Î ± ³ μ Ê ³ Ê ²μ ŠμÔËË Í ÉÒ ³μ ² ²μ± ²Ó μ
Ó³ Ÿ , º 6Ä7(176Ä177).. 823Ä Œ. Œ ²±μ,,.. É ²,.. μ ²Ó,.. Íμ,.. ŠÊÉÊ μ,.. μ ±μ,.. ÒÏ
 Ó³ Ÿ. 2012.. 9, º 6Ä7(176Ä177).. 823Ä837 Œ ˆŠ ˆ ˆ Š ƒ Š ˆŒ Š Œ ƒ Š Š Š ˆŒ ˆ ˆ. Œ. Œ ²±μ,,.. É ²,.. μ ²Ó,.. Íμ,.. ŠÊÉÊ μ,.. μ ±μ,.. ÒÏ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê μë ± Ê É É ³.. Š² ³ É Ì ±μ μ, μë Ö μ Éμ É μ μ
Ó³ Ÿ. 2012.. 9, º 6Ä7(176Ä177).. 823Ä837 Œ ˆŠ ˆ ˆ Š ƒ Š ˆŒ Š Œ ƒ Š Š Š ˆŒ ˆ ˆ. Œ. Œ ²±μ,,.. É ²,.. μ ²Ó,.. Íμ,.. ŠÊÉÊ μ,.. μ ±μ,.. ÒÏ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê μë ± Ê É É ³.. Š² ³ É Ì ±μ μ, μë Ö μ Éμ É μ μ
Tegn og tekst. Et representert tegn kan vises på flere måter. Noen definisjoner. Enda noen definisjoner. \yvind og ]se N{rb}? a a a.
![Tegn og tekst. Et representert tegn kan vises på flere måter. Noen definisjoner. Enda noen definisjoner. \yvind og ]se N{rb}? a a a. Tegn og tekst. Et representert tegn kan vises på flere måter. Noen definisjoner. Enda noen definisjoner. \yvind og ]se N{rb}? a a a.](/thumbs/62/47219195.jpg) o o {rb} rprr på r år o prpp rpro r r rr rpro o r o or α r o or bor brp or b rr på ppr r r r r r rrr år på o oroooro o r or o br å r r pår r r orør p o b b år r å r o o o rprrr o p o rprrr o or op r r
o o {rb} rprr på r år o prpp rpro r r rr rpro o r o or α r o or bor brp or b rr på ppr r r r r r rrr år på o oroooro o r or o br å r r pår r r orør p o b b år r å r o o o rprrr o p o rprrr o or op r r
prog.f prog.il prog.s
 ÇÚÖÚÛ Ó Ø ÔÖØ ÁÎ ÊØÚ ÄÌÊ ÈÖÓØ ÇÆË ÇÔØÑÞÒ ÓÑÔÐÖ ÓÖ Ñ ÔÔÐØÓÒ ÈØÖ ÅºÏº ÃÒÒÒÙÖ ÄÒ ÁÒ ØØÙØ Ó ÚÒ ÓÑÔÙØÖ ËÒ ÄÒ ÍÒÚÖ ØÝ ÆÐ ÓÖÛ ½ ¾ ÄÒ Ì ÆØÖÐÒ ÔØÖÐ ºÒÐ ØÖØ Ì ÔÔÖ ÔÖ ÒØ Ò ÓÚÖÚÛ Ó Ø ØÚØ ÖÖ ÓÙØ ÛØÒ Ø ËÈÊÁÌ ÔÖÓØ ÇÆË
ÇÚÖÚÛ Ó Ø ÔÖØ ÁÎ ÊØÚ ÄÌÊ ÈÖÓØ ÇÆË ÇÔØÑÞÒ ÓÑÔÐÖ ÓÖ Ñ ÔÔÐØÓÒ ÈØÖ ÅºÏº ÃÒÒÒÙÖ ÄÒ ÁÒ ØØÙØ Ó ÚÒ ÓÑÔÙØÖ ËÒ ÄÒ ÍÒÚÖ ØÝ ÆÐ ÓÖÛ ½ ¾ ÄÒ Ì ÆØÖÐÒ ÔØÖÐ ºÒÐ ØÖØ Ì ÔÔÖ ÔÖ ÒØ Ò ÓÚÖÚÛ Ó Ø ØÚØ ÖÖ ÓÙØ ÛØÒ Ø ËÈÊÁÌ ÔÖÓØ ÇÆË
ÄÒÖØÒ ½º½ ÃÖØÒ ½ ÄÒÖØÒ ½º½º½ ÄÒÖØ ½º½ ÃÖØÒ ÄÒÖØÒ ½º½º¾ ËØÖÒÖØ ½º½º ÈÖÓÚÒÞÒ
 ½ ¾ ÆÓÖ ¹ ÌÝ ÌÝ ¹ ÆÓÖ ÊØ ÙÒ ÁÒÓ ÅÖ ØÒÖ ¾º ÖÙÖ ¾¼¼ ÁÒÐØ ÚÖÞÒ ÁÒÐØ ÚÖÞÒ ½ ÄÒÖØÒ ½º½ ÃÖØÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º½ ÄÒÖØ º º º º º º º º º º º º º º º º º º º
½ ¾ ÆÓÖ ¹ ÌÝ ÌÝ ¹ ÆÓÖ ÊØ ÙÒ ÁÒÓ ÅÖ ØÒÖ ¾º ÖÙÖ ¾¼¼ ÁÒÐØ ÚÖÞÒ ÁÒÐØ ÚÖÞÒ ½ ÄÒÖØÒ ½º½ ÃÖØÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º½ ÄÒÖØ º º º º º º º º º º º º º º º º º º º
ÄÒÖØÒ ½ ÃÖØÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º½ ÄÒÖØ º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º½ ËØ
 ¹ ÌÝ ÆÓÖ ¹ ÆÓÖ ÌÝ ¾ ½ ÊØ ÙÒ ÁÒÓ ÅÖ ØÒÖ ¾º ÖÙÖ ¾¼¼ ÄÒÖØÒ ½ ÃÖØÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º½ ÄÒÖØ º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º½ ËØÖÒÖØ
¹ ÌÝ ÆÓÖ ¹ ÆÓÖ ÌÝ ¾ ½ ÊØ ÙÒ ÁÒÓ ÅÖ ØÒÖ ¾º ÖÙÖ ¾¼¼ ÄÒÖØÒ ½ ÃÖØÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º½ ÄÒÖØ º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º½ ËØÖÒÖØ
DRIFTSANALYSER 2012/2013 FORELØBIGE RESULTATER
 DRIFTSANALYSER FORELØBIGE RESULTATER A B C D E F C G H E I J K L B K F G K! " # $ %! & ' ( ) ( * + #, -! &!. & ) /! ( / ) - 0 1 - ' #.! ( ( * ' 1 2 ( (! 3 4 " (! - 5 6!! 7 % ' # 7 4 " (! - 1 2 # 7 4 8-1
DRIFTSANALYSER FORELØBIGE RESULTATER A B C D E F C G H E I J K L B K F G K! " # $ %! & ' ( ) ( * + #, -! &!. & ) /! ( / ) - 0 1 - ' #.! ( ( * ' 1 2 ( (! 3 4 " (! - 5 6!! 7 % ' # 7 4 " (! - 1 2 # 7 4 8-1
7 Global Linkages and Economic Growth
 7 Global Linkages and Economic Growth Y t = F(K t,e t L t ), (1) Y t C t = S t = sf(k t, E t L t ). (2) K t+1 K t = sf(k t, E t L t ) δk t, (3) Foundations of International Macroeconomics (297) Chapter
7 Global Linkages and Economic Growth Y t = F(K t,e t L t ), (1) Y t C t = S t = sf(k t, E t L t ). (2) K t+1 K t = sf(k t, E t L t ) δk t, (3) Foundations of International Macroeconomics (297) Chapter
USER GUIDE. RRD Silencioso
 USER GUIDE RRD Silencioso!"#$%&'()*+, -,,$.//01$02$%&'()*+,3()4 USER GUIDE 56789:;?@ =9=8 :?B69C>=:6? >D 9EFG:9E@ ii USER GUIDE H IJKLMNOPKQMJRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRS
USER GUIDE RRD Silencioso!"#$%&'()*+, -,,$.//01$02$%&'()*+,3()4 USER GUIDE 56789:;?@ =9=8 :?B69C>=:6? >D 9EFG:9E@ ii USER GUIDE H IJKLMNOPKQMJRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRS
Offentlig utvalg for punktskrift, OUP Norsk standard for 8-punktskrift punktskrift 24. oktober 2004 sist endret
 Offentlig utvalg for punktskrift, OUP Norsk standard for 8-punktskrift punktskrift 24. oktober 2004 sist endret 19.10.2007 Desimal Hex Beskrivelse Tegnets utseende Punktkode 0 0000 4578
Offentlig utvalg for punktskrift, OUP Norsk standard for 8-punktskrift punktskrift 24. oktober 2004 sist endret 19.10.2007 Desimal Hex Beskrivelse Tegnets utseende Punktkode 0 0000 4578
NEK NK9 Elektrisk utstyr for baner
 NEK NK9 Elektrisk utstyr for baner Geir L. Eriksen Formann NK9 Jernbaneverket Stab Sikkerhet Arbeidet i JBV i snart 45 år og vært formann for NEK NK9 i ca 20 år I begynnelsen. Dagens elektrifiserte jernbane
NEK NK9 Elektrisk utstyr for baner Geir L. Eriksen Formann NK9 Jernbaneverket Stab Sikkerhet Arbeidet i JBV i snart 45 år og vært formann for NEK NK9 i ca 20 år I begynnelsen. Dagens elektrifiserte jernbane
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ Ï Ìμ μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2015.. 46.. 1 Š ˆ Š Š Š.. Ï Ìμ μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 167 Œ 168 Šμ É Ê±Í Ö 168 μ É Ò Ì ±É É ± 171 ˆ ˆ Šˆ 172 ˆμ Í Ö μ, μ μ Ê ² 172 Í É Ö 173 ³Ò μéò 178 ƒ μ Ò ³ 180 ² Ö ³ É μ μ± Ê ÕÐ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2015.. 46.. 1 Š ˆ Š Š Š.. Ï Ìμ μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ 167 Œ 168 Šμ É Ê±Í Ö 168 μ É Ò Ì ±É É ± 171 ˆ ˆ Šˆ 172 ˆμ Í Ö μ, μ μ Ê ² 172 Í É Ö 173 ³Ò μéò 178 ƒ μ Ò ³ 180 ² Ö ³ É μ μ± Ê ÕÐ
! " # $ % & ^Pv`!$ x âîv7ç È'Ç È b j k Æ' z{3 b jkæ b ÇÈÉÊ&( )! c q r É. xy+ - Êlm l D E ` &! D E â î #" ' #$ '#! v( D/Ev A B x y&?
 ! " )*+,-/ 0 $$ "#2!$3456578 56 34 " 56!< >?@ABCDE,-
! " )*+,-/ 0 $$ "#2!$3456578 56 34 " 56!< >?@ABCDE,-
We bring information to life
 1 2L o k a l t t i l s t e d e, n o r d i s k s t y r k e We bring information to life #EVRYsmartkontor Velkommen til frokostseminar! 08:30 Registrering og lett frokost 09:00 Velkommen. 09:05 -Hva har
1 2L o k a l t t i l s t e d e, n o r d i s k s t y r k e We bring information to life #EVRYsmartkontor Velkommen til frokostseminar! 08:30 Registrering og lett frokost 09:00 Velkommen. 09:05 -Hva har
ˆ ˆŒˆ ˆŸ Š Œ ƒˆˆ 60Ä1000 ŒÔ ˆ ˆŠ ˆŸ Ÿ ˆ ˆ ˆ ˆ Š ˆ Š ˆŠˆ
 Ó³ Ÿ. 2017.. 14, º 1(206).. 144Ä163 ˆ ˆŠ ˆ ˆŠ Š ˆ ˆ ˆŒˆ ˆŸ Š Œ ƒˆˆ 60Ä1000 ŒÔ ˆ ˆŠ ˆŸ Ÿ ˆ ˆ ˆ ˆ Š ˆ Š ˆŠˆ.. É ³μ μ 1,. Œ. ˆ μ,.. ˆ μ,.., ƒ.. Ö μ ƒ É Ê ± É ÉÊÉ Ö μ Ë ± ³... Šμ É É μ ˆ ŠÊ Î Éμ ± É ÉÊÉ, ƒ
Ó³ Ÿ. 2017.. 14, º 1(206).. 144Ä163 ˆ ˆŠ ˆ ˆŠ Š ˆ ˆ ˆŒˆ ˆŸ Š Œ ƒˆˆ 60Ä1000 ŒÔ ˆ ˆŠ ˆŸ Ÿ ˆ ˆ ˆ ˆ Š ˆ Š ˆŠˆ.. É ³μ μ 1,. Œ. ˆ μ,.. ˆ μ,.., ƒ.. Ö μ ƒ É Ê ± É ÉÊÉ Ö μ Ë ± ³... Šμ É É μ ˆ ŠÊ Î Éμ ± É ÉÊÉ, ƒ
We bring information to life
 1 2L o k a l t t i l s t e d e, n o r d i s k s t y r k e We bring information to life Velkommen til «Hot i Ålesund»! 12:00 Registrering 12:30 Velkommen 12:40 Kontoret ditt blir et #SMARTkontor 13:00 Mulighetene
1 2L o k a l t t i l s t e d e, n o r d i s k s t y r k e We bring information to life Velkommen til «Hot i Ålesund»! 12:00 Registrering 12:30 Velkommen 12:40 Kontoret ditt blir et #SMARTkontor 13:00 Mulighetene
ﺪ ﻩ ﻋﺍ ﻮﹶ ﻭ ﻗ ﻪ ﹾﻘ ﹾﻟ ﻔ ﺍ ﹺﻝ ﻮ ﹸﺃ ﺻ ﹸ ﻣ ﺔ ﻮﹸ ﻈ ﻣ ﻨ $ ﺡﺮﺷ! " ' (# $% & )*! +,!* -
 م ن ة ظو م ل ا ا ل صو ق ف ه و ع وا ق و ه د $ شرح ٢ الا ول] [الدرس :$, : $ $, : ; $, موقع التف ري غ للدرو س الع لمية والبحوث الشرعي ة Ï Î Í Ì ٣,,,,,, : :, :,, :,, : $,,,,,, : :,, :,,:ÑÐ, :,,,, :,, :,,,,,,,,
م ن ة ظو م ل ا ا ل صو ق ف ه و ع وا ق و ه د $ شرح ٢ الا ول] [الدرس :$, : $ $, : ; $, موقع التف ري غ للدرو س الع لمية والبحوث الشرعي ة Ï Î Í Ì ٣,,,,,, : :, :,, :,, : $,,,,,, : :,, :,,:ÑÐ, :,,,, :,, :,,,,,,,,
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ ± É,. ˆ. ˆ ± Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2004.. 35.. 2 Š 621.039.5; 550.837 ƒ ˆŸ Š Œ.. ± É,. ˆ. ˆ ± Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê ˆ 349 Š ƒ ƒˆ Šˆ Œ ˆ ˆ ƒ ˆ Šˆ Š ˆ 350 Ÿ œ Œ Š Œˆ ˆ ˆ ˆ ŠˆŒˆ Œˆ ƒ ˆ Œ ˆ 366 ˆ œ ˆ Š ƒ - ˆ ˆˆ Œ ƒ ƒˆˆ ˆ ƒ
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2004.. 35.. 2 Š 621.039.5; 550.837 ƒ ˆŸ Š Œ.. ± É,. ˆ. ˆ ± Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê ˆ 349 Š ƒ ƒˆ Šˆ Œ ˆ ˆ ƒ ˆ Šˆ Š ˆ 350 Ÿ œ Œ Š Œˆ ˆ ˆ ˆ ŠˆŒˆ Œˆ ƒ ˆ Œ ˆ 366 ˆ œ ˆ Š ƒ - ˆ ˆˆ Œ ƒ ƒˆˆ ˆ ƒ
P ²Êϱ 1,..Šμ ² ±μ 1,.. μ Î 1,2 ˆ ˆŸ. ² μ Ê ² μ Ì μ ÉÓ. É μ ±, Ì μé μ Ò É μ Ò ² μ Ö. ÍÒ Œμ ±μ ±μ μ μ Ê É μ μ Ê É É ³. Œ..
 .. ²Êϱ 1,..Šμ ² ±μ 1,.. μ Î 1,2 ˆ ˆ Œ ˆ ˆŸ Š ˆ : ˆ ˆ ˆ ˆ? P14-2011-18 ² μ Ê ² μ Ì μ ÉÓ. É μ ±, Ì μé μ Ò É μ Ò ² μ Ö 1 Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê, μ Ö 2 ÊÎ μ- ² μ É ²Ó ± É ÉÊÉ Ö μ Ë ± ³... ±μ ²Ó- ÍÒ Œμ ±μ ±μ
.. ²Êϱ 1,..Šμ ² ±μ 1,.. μ Î 1,2 ˆ ˆ Œ ˆ ˆŸ Š ˆ : ˆ ˆ ˆ ˆ? P14-2011-18 ² μ Ê ² μ Ì μ ÉÓ. É μ ±, Ì μé μ Ò É μ Ò ² μ Ö 1 Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê, μ Ö 2 ÊÎ μ- ² μ É ²Ó ± É ÉÊÉ Ö μ Ë ± ³... ±μ ²Ó- ÍÒ Œμ ±μ ±μ
FORBUND DISCIPLIN POINT PLACERING Navn
 PERIODE MESTER- SKAB FORBUND DISCIPLIN POINT PLACERING Navn 13. januar-29. januar VM Håndbold Herre 0 10.plads Mads Mensah Larsen, Henrik Toft Hansen, Casper U. Mortensen, Jesper Nøddesbo, Niklas Landin
PERIODE MESTER- SKAB FORBUND DISCIPLIN POINT PLACERING Navn 13. januar-29. januar VM Håndbold Herre 0 10.plads Mads Mensah Larsen, Henrik Toft Hansen, Casper U. Mortensen, Jesper Nøddesbo, Niklas Landin
